The Pythagoreans

Life and Works

Little is known about the life of Pythagoras. Born on the island of Samos, he emigrated to Magna Graecia, a Greek colony in southern Italy. [i] A student of the Babylonians, Egyptians, Indians or Zoroastrians, he became a statesman of Croton [ii] and developed a large following. He has been labeled mystic, guru, shaman, philosopher, cosmologist and scientist. Perhaps all of these labels are not quite true. His floruit occurred around 532 B.C. and so he was born perhaps around 572 B.C. He may have met Thales as an old man and he may have spent time studying in Egypt. Plato [iii] and Aristotle [iv] mention him indirectly because his actual contributions were in doubt, as they are today:

The learning of many things does not teach one intelligence; if it did it would have taught Hesiod and Pythagoras, and again Xenophanes and Hecataeus. (Diogenes Laertius IX, I) Pythagoras...engaged in learning by inquiry more than all other men and, having made a selection of these writings, claimed a wisdom of his own, badly wrought and superficial. (Diogenes Laertius VIII, 6)

Pythagoras founded a religious order that advocated vegetarianism and espoused metempsychosis, a cosmic system of reincarnation. Again, Diogenes Laertius:

What [Xenophanes] says about Pythagoras goes like this: 'Once they say that while passing a puppy that was being mistreated he had compassion and said: “Stop, do not hit it; for it is the soul of a friend that I recognized when I heard it crying.” (Diogenes Laertius VIII, 36). [Pythagoras] says the soul is immortal; next that it changes into other kinds of creatures; that in certain cycles things that have occurred again come to be, and that nothing is absolutely new; and finally, that there is need to believe all ensouled things are of the same race. Pythagoras appears to have been the first to import these beliefs to Greece. (Porphyrius, Vita Pythagorae 19) Diogenes Laertius (VIII, 4-5) also says that Pythagoras recalled four of his incarnations.

The Pythagorean community forbade divulging of secrets [v] because Pythagoras and his followers wrote nothing and communicated orally. Thus little was written by the order initially. His followers for one reason or another developed a precedent of attributing insights to their master even when new ideas arose after his death and so at least some mathematical insights attributed to Pythagoras were not actually his. After his death his school separated into two sects. The one adhered to the mystical metempsychosis, the other – being mathematicians – concentrated on applying number to reality.[vi] No reliable source of Pythagoras' own engagement in scientific inquiry exists, and so we talk of “Pythagoreans” because the ones most likely responsible for the mathematical insights attributed to Pythagoras are his followers. [vii] Still, Pythagoras himself perhaps deserves credit for discovering that principal musical intervals can be expressed in numeric ratios between the first four integers. [viii]

First Principles

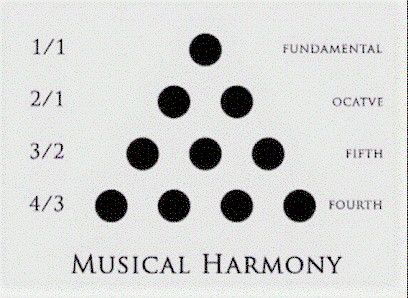
Most probably, Pythagoras discovered the ratio of musical intervals by using a monochord, a single-stringed ancient device that measured sound frequencies. He may have examined its sounds and learned what musicians knew about the scales; [ix] thus an inductive and empirical aspect of his discovery some claim is an experiment. [x] The ratios he measured are the octave = 2:1, the fifth = 3:2, and the fourth = 4:3. The octave is an interval between one pitch and another in half or double its frequency. Thus, the ratio of 2:1. A fifth and fourth are like intervals of different spacing. One may explain much of Pythagoras' own inspiration through his thought about the musical scale. There are low and high pitches. The low pitches are vibrations that are slow and the high pitches are those that are fast. On the musical scale the different vibrations create different pitches. When one travels up or down the scale one-half or twice as much, one finds a pitch that is similar to a pitch positioned that distance. Now, we measure these pitches by hertz. So, a pitch of 50 hertz will be an octave of a pitch of 100 hertz. The same is true of a pitch at 200 hertz. The ratio of the scale determines the distance from one pitch to another. The ratio for a fifth is, as above, 3:2, and the ratio for a fourth is 4:3. The musical scale may be thought of as an unlimited series because of an unlimited number of vibrations while the points on the scale and their ratio is a measurement determined by number and therefore bounded, limit that is. That is to say, number makes a boundary that produces a specific pitch. Number demarcates and therefore makes things, and Pythagoras theorized that all of the objects of the universe actually are the proportion of some ratio upon what may be called the unlimited. [xi] Most of the Pythagorean insights that arise from his initial thought are applications of some kind of mathematical measurement to all objects in the universe.[xii] For example, the Pythagoreans believed that the number ten was the nature of number:

The nature of number is ten. All Greeks...count up to ten, and having come to ten return again to the unit. And again, Pythagoras says, the power of the number ten lies in the number four, the tetrad. This is the cause: if one starts at the unit and adds successively the numbers up to four, one will come to the number ten; and if one overshoots the tetrad, one will exceed ten too. Thus, if one takes the unit, adds two and three and to these adds four, one will make up the number ten. The result is that number as a unit exists in the number ten, but potentially in the number four. (Aetius I, 3, 8)

They conceived the number one as a whole and after the whole unit of ten is reached the counting begins again, added to the number of ten-units that have already been counted. Because the ten-unit is the renewal of the counting, that amount of numbers is fundamental to the measurement of mathematics; is it again the unit. The number four is the number of numbers that comprise the unit of ten and it is also the number that contains one, two and three (in a seemingly literary sense) and thus produces the new unit, a unit which is the foundation of all numbers. In this sense it seems that the Pythagoreans thought of four as being potentially ten. 1 is not truly a number because it is not yet plural; 2 is the beginning of even numbers, and 3 the beginning of odd. 5 has the distinction of being the first product of the first principles. [xiii] The Tetractys of the Decad (essentially the number 10) is a visual representation of this conception of number.

One can see not only the addition of four numbers that comprise ten in interesting ways, [xiv] but also the initial insight into the musical scale fits conveniently into the scheme of this conception of number, the octave and the fifth as well as the fourth being set within the ten-unit. It is no wonder that Pythagoras conceived of material reality as itself composed of number and number composed of music and thus the universe was conceived as musical.

Causation and Cosmology

Something about number was not only a part of each thing; it was logical constant. Number had determined something essential about the musical scale. It was not merely a tool for measurement, but its ratio was the musical scale. Not only was number always able to be applied with certainty; it was divine in its certainty. [xv] Number becomes vital in the comprehension of material reality because one only needs to apply the proper number or set of numbers to an object in order to know fundamentally what it is. Justice had a specific number, as did a line, a plane and a solid.

Since of these principles numbers are by nature the first, and in numbers [Pythagoreans] seemed to see many things most similar to existing things and things coming to be, more than in fire and earth and water so that this sort of manifestation of numbers is justice and another sort mind and reason, and another being opportunity–and each of the others similarly manifest so to speak.... (Aristotle Met. A5, 985b23).

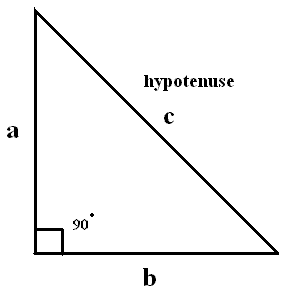
Aristotle claims that the Pythagoreans confused abstract number with objects. In other words, numbers themselves were supposed to have spatial extension. While such a misapplication led the Pythagoreans into many imaginative corners, certain calculations applied as measurement of spatial extension operated with seeming flawlessness. One can see how the musical scale and the Decad impressed, but the Pythagorean theorem, still used today, is one representative example of the potency for lasting influence and truth in Pythagoras' perspective on number: the square on the hypotenuse of a right-angled triangle is equal to the sum of the squares on the sides enclosing the right angle (A²+B²=C²). [xvi] The formula is relatively easy. Given a right triangle, the sum of the squares of the two sides opposite the hypotenuse (the side opposite to the right angle) is equal to the square of the hypotenuse.

So, here if a = 3 and b = 4, then c = 5. The unit of measure makes no difference and this formula arrives at the required number no matter the size of the triangle, as long as one of the angles is a right angle. Most important for our purposes, it is accurate whether there is an actual triangle present or not. It seems the ability of number to perform universal tasks like the musical ratios and the “Pythagorean” theorem is what convinced Pythagoras and his followers that they had a means to access a fundamental aspect of all things. One needed only to discover the number or ratio that was the shape, mass, depth et cet. of things as well as the number that was the objects themselves in order to find its essence, fundamental and applicable on any occasion. Number was bounded and it operated with the boundless. No other principle or element could be applied so universally. Aristotle sums up their conception:

...the Pythagoreans have said...that there are two principles, but added this much, which is their specific thing, that they thought the bounded and the limitless and the one were not certain other natures, such a thing as fire or earth or some other sort of thing, but that the limitless itself and the one itself were the very existence of which things they are predicated. This is why number was the very existence of all things. (Aristotle Met. A5, 987a13)

It is the universal application that we must remember because if and when the Pythagoreans arrived at proofs, they were discovering theorems that were deductive. In other words, the logic they were using compelled them to arrive at specific conclusions. We have seen that deduction is precisely that: if one accepts the premises (in this case the increments and their measurements), then the conclusion naturally follows. Numbers were, of course, responsible for the potential reproduction of their findings and thus a constant, fundamental principle. Qualities of numbers were for Pythagoreans characteristics of the material universe. Oddness and evenness were the limit (light or fire) and the unlimited (air, void, or space) respectively, [xvii] as we have seen in the determination of the musical scales. Their insight into the musical scale led them to believe they were able to find similar applications of number, or the numbers themselves, in whatever they analyzed. Limit was oddness, unity, rest, goodness and the unlimited was evenness, multiplicity, motion, bad. The whole of their dualism relied upon this mathematical underpinning to opposites. [xviii]

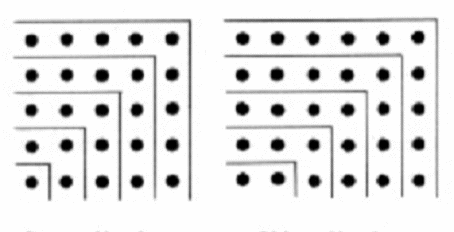
The above figure shows the gnomon, or shapes comprised of points. As we said above, the Pythagoreans thought of numbers as actual points. In other words, they seemed to believe that numbers have magnitude in themselves. In the left figure the square is comprised of odd-numbered points stacked around one another. It remains a square no matter what odd number is added to it, and a clear line divides it into halves. The Pythagoreans believed that this number represents limit and thus a figure that possesses a beginning, middle and end. The addition of an odd number of points is necessary to compose a new square, but always there will be a new square, given the addition of a new set of odd numbers. Only the size changes. In the figure on the right, the rectangle, even numbers are added in order to compose a figure, but the ratio changes with each addition of an even number. Pythagoreans took this altering of ratio as a sign of indefiniteness; also there is no clear middle part of this construction. Thus, they associated evenness with the unlimited, which lacked necessary parameters of a more balanced constant form, like the square:

[The Pythagoreans] meant by the limitless even number, 'because everything even',...'is divisible into equal things, and the thing that is divisible equally is limitless with respect to division in two; for halving into equals continues (without limit), but the addition of the odd makes a limit; for it prevents the division of it into equal things'. In this way the commentators attach the limitless to the even in respect of division into equal things, and it is clear that they take limitless division in terms not of numbers but of magnitudes.... (Simplicius Physics 455, 20)[xix]

A similar way of applying numbers and their quantity to the musical scale and the Pythagorean theorem also applied to everything. [xx] One needed only to find what that application is. The difficulty in this kind of thinking, of course, is that number is assumed to have already some kind of spatial magnitude, or that number generates spatial magnitudes. After that assumption the formulas are constructed. Aristotle critiques their position:

...that bodies are composed of numbers, and that this number is mathematical, is impossible. For to speak of magnitudes as indivisible is not true; as much as there may be magnitudes that exist in this manner, units at any rate have no magnitude; and how is it possible that a magnitude come from indivisibles? But certainly arithmetical number, at any rate, is unitary, and they [Pythagoreans] say number is real things; their propositions they apply to bodies as if they consisted of those numbers. (Aristotle Met. M8, 1083b8) [xxi]

Some scholars assert [xxii] that Pythagoreans believed number to be a kind of atom and that Greeks were slow to think of things as having no spatial extension, but atomistic principle of number and spatial extension may not be precisely what Pythagoreans intended. Number may have possessed a more metaphysical characteristic. Numbers may have been necessary to produce many kinds of substantiality from seemingly insubstantial abstraction. Fire and earth have a different principle than justice or soul, yet Pythagoreans seem to have believed that number was responsible for the genesis of each.

Whether the Pythagoreans attribute coming-to-be to [eternal things] or not there is no need to doubt; for clearly they say that once the one had been constructed, either out of planes or of surface or of seed or of [other] things they are at a loss to say, immediately the nearest part of the limitless began to be drawn in and limited by the limit. (Aristotle Met. N3, 1091a12)

It may be that they thought of number as being capable of generating extension as well as justice, thought and the like:

For since the dyad is the first distance (for the unit first made distance into the dyad, and in this way to the triad and the successive numbers), if we mark out the line, the Pythagoreans say, it is not necessary to say that it is quantity in one direction, but a line is the first distance made. (Alexander Met. 512, 37)

Yet if one believes Aristotle, a sometimes notorious critic, they never articulated precisely how that genesis took place. Void existed for the Pythagoreans and it performed a necessary function, coming from the unlimited:

The Pythagoreans...held that void exists and that [a kind of] breath...and void enter from the limitless into the sky itself as if inhaling and that the void marks out the natures of things, the void being a kind of separating and distinguishing factor of successive things. This is the first thing among the numbers; for the void demarcates their nature. (Aristotle Physics D6, 213b22)[xxiii]

It seems to have been a negative aspect of things that distinguished parameters. Naturally, void would come from an indefinite aspect of reality, and the unlimited was that aspect for the Pythagoreans. Though they may have conceived of number as possessing more than one substantiality, we are at least justified in claiming that the Pythagoreans thought of number as the beginning of spatial extension, as long as the point itself has extension:

For 1 is the point, 2 the line, 3 the triangle and 4 the pyramid. All these are the first things, the principles of individual things of the same kind...and the same things [come to be] in generation too; for the first principle in magnitude is the point, the second the line, the third surface and the fourth the solid. (Speusippus ap. Theologumena Arithmeticae p. 84, 10 de Falco) [xxiv]

The Pythagoreans also held a conception of the universe based upon the initial insight of the musical intervals that the entire universe made sound:

It is clear from these things that the assertion that a harmony came to be from the stars carrying themselves about, i.e. that the sounds they make are consonant...is not true. It seems to some [Pythagoreans] that a sound comes to be from bodies of such a size being carried, since locally things having neither equal bulk [to the celestial beings] nor being carried by such a speed [actually produce] sound; Also, when the sun and the moon...and the mass and great number of stars are moving with so rapid a motion, it is not possible that a sound of such magnitude not come to be. Positing these things and that their speeds, as measured by their distances, have the ratios of musical consonants, they assert that the [musical] sound of the stars being carried around in a circle is a harmony. (Aristotle de caelo B9, 290b12)

According to Aristotle the Pythagoreans adhered to their theories rather than observation:

Most say that the earth lies at the center of the universe,...but the...Pythagoreans say otherwise. At the center...is fire, and the earth, one of the stars being carried in a circle around the middle, makes night and day. Still another earth opposed to this one they construct, which they call by the name counter-earth, not seeking reasoning and causes pertaining to appearances but forcing the appearances upon some reasoning and opinions of their own. But to many others it would be agreed that there is no need to assign to the earth the middle place, fitting their belief not on appearances but rather on arguments. They think that the most honored place befits the most honored thing: and fire is more honored than earth and limit more honored than intermediate, and the outermost point and the middle are limits. The result of reasoning from these things is that they do not think it [the earth] lies in the middle of the sphere, but rather fire [does]. (Aristotle de caelo B13, 293a18)

The very universe, then, is not only configured differently than common perception allowed, but it produces vibrations by its very essence and is therefore musical. In this manner the Pythagoreans took Anaximander's three wheels (sun, moon and stars) that composed the universe and gave them ratios;[xxv] the earth was shaped like a sphere because of the solid figures it is most beautiful. The Pythagorean cosmology begins when the numbers are generated as the unlimited is taken in (breathed in) by the limit. [xxvi] Notice that in a proto-scientific manner the Pythagoreans make use of number as a means to measure and understand the universe. They do not use an hypothesis and then test it, but they seem to have believed that number not only measured the universe but was that measure. The initial insight of the musical scale applied in a fundamental way to points, lines, planes, plane figures, solids and then other topics like the cosmos. Remember that for them number also applied to abstractions like justice, the soul, god and love. The very universe itself is musical, and perhaps one reason Pythagoreans adhered to this assertion is that such a perspective is somewhat romantic and literary. There is a charm to comprehending the whole of the universe in terms of music.

Argumentation

It remains to evaluate some small part of Pythagorean argumentation and see how it applies precisely. We take only the beginning insight of the musical scale and the Pythagorean theorem as our points of discussion. Number seems to have been applied as a tool in the measurement of the musical scale and the Pythagorean theorem. Yet, number is applied to everything possible because the unlimited and limit seemed to be a fundamental part of measurement and calculation. One mistake was that the Pythagoreans took measurement as reality. In other words, even in antiquity Aristotle and others took numbers as abstractions; we have seen Aristotle say as much. The Pythagoreans wished to apply them to reality as the objects they analyzed. Number provides a foundation for the determination of parameters certainly in shapes and abstract solids, but there is no clear argument that number actually is existing solids or abstract notions like justice, and application of number to certain things simply does not work. Thus, Aristotle's complaint. There was, however, a deductive aspect to Pythagorean thinking that must have been seductive. The application of number to right triangles had produced a calculation that unerringly, seemingly, produced the correct assessment no matter the size or presence of a right triangle. Numbers may have seemed to be at once eternal and substantial in every sense because they were capable of measuring despite size or even manifestation.

All things measurable by formulations of number are things representative of all parts of reality.
All right triangles are things measurable by formulations of number.
All right triangles are things representative of all parts of reality.

This argument is something like the attitude Pythagoreans seem to have taken. Number as fundamentally all things is assumed once the insight into right triangles and its implications have been observed. One has only to determine how. Imaginative use of number application abounded, and sometimes their efforts came to fruition, as in the Pythagorean theorem. Other times their efforts were playful, as in four points actually being a solid. Yet, one cannot apply number to all things simply because its application to a right triangle or a musical scale seems to have revealed something hidden in them. The revelation of what is a right triangle is not the revelation of any given thing or object. Nevertheless, the use of numbers in the musical scale as well as the Pythagorean theorem is perfectly legitimate. One cannot adequately represent its calculation in a syllogism, but the reasoning makes seemingly impervious connections. In each and every case of a right triangle, given certain conditions, where C is the hypotenuse and where A and B are the opposing lines that comprise the right angle, the formula A² + B² = C² is true. One must think in terms of deduction compared to induction. Math is inherently deductive. 8 x 4 always equals 32, at least in traditional mathematics. There is no other conclusion to draw as there are no other conclusions to draw when other operations are in order. Addition, subtraction, multiplication, division all give one answer. This simple truth makes mathematics absolutely certain in its own realm. One may then apply mathematical reasoning to things in the universe, but as we have seen the application is partial or limited and an element of observation and thus empiricism is necessary. Again, we cannot form a mathematical calculation of justice or of love. The basic outlines of solids are amenable to mathematical calculation, but numbers are not in objects. Objects are in objects. Pythagoreans in their apparent excitement attempted to apply imaginatively a very potent deductive system to things that do not lend themselves completely to such a system. In other words, math as they employed it seems to be limited to measurement of material reality and Pythagoreans wished to transform math into an ontology, or some system that is the study of being. Here is one of the primary divergences of philosophy and science. Science (here physics) is not an ontology; it is a measurement of an object, or a thing, as it exists materially or as come kind of process. Pythagoreans thought that what is meta-material about reality and what is material were the same. Therein lies their mistake. Perhaps they were aware of the difficulties of their position, but given that we have only some scattered references from ancient scholars and a not always reliable Aristotle to tell us, we simply cannot make a certain determination. The lasting power of Pythagoreanism is that it gave rise to measurement by number, not equation of number with being.

One most important thought about the Pythagoreans: the Pythagorean theorem was a logical constant for the ancients. We will see that as scientific progress continued the use of mathematics in revealing unseen aspects of the universe grew. Yet, mathematical systems are systems of logic. Systems of logic need solid foundations upon which they make assertions about reality. Logical constants in such systems are essential in creating solid connections and reasoning in a strong way. The old analogy of a building applies. A building with a solid foundation stays up. The logical constants are the solid foundation, or the reference points used to make calculations about how objects react to certain conditions and what they are. There are many operationally logical constants in scientific reasoning: sine, cosine, tangent, Pythagorean theorem are only some examples. These logical constants are so regular as to be reliable to insert into hypotheses, though we are finding that constants are not as constant as once thought. And science has used them ever since humans realized that these logical constants have a firm foundation. In fact, we have even seen that logical constants like the Pythagorean theorem do not even need to apply to existing things. The formula itself will be true no matter what the state of the universe is, according to ancient reasoning. That is how reliable the formula of the Pythagoreans is, and the Pythagoreans began the process of deductive reasoning along with Parmenides and Zeno. [xxvii] Modern science makes use of these logical formulations in order to form theoretical, mathematical calculations that are then tested. Here lies the difference between theoretical and applied mathematics. One can see easily how lasting and incredible such an insight as the Pythagorean theorem has been and continues to be. It has not only endured thousands of years of scrutiny. It also has found its way into the modern world of hyper-mathematical experimentation. Though Pythagoras did not come up with all the insights attributed to him, his one insight endures. It seems, in fact, to be constant.

[i] See Geoffrey Lloyd.
[ii] Diog. L. VIII, 3.
[iii] Plato, Rep. 600 A-B.
[iv] Aristotle, Met. A5, 986a 30 and Rhet. B23, 1398b 14.
[v] Iambl. V.P. 199 (DK 14, 17).
[vi] 1 was mind; 2 opinion; 3 the number of the whole; 4 justice; 5 Marriage; 6 ?; 7 the right time; 8?; 9 justice; 10 perfect. Aristotle reviews these but could not determine 6 or 8. For more, see Cornford (1922 and 1923).
[vii] Specifically Philolaus, Archytas and Eudoxus. The works of these men are lost, but referred to in later commentaries and other works. Some believe that Pythagoras deserves credit for creating a kind of science. Reviel Netz seems correct in saying that at least Pythagoras combined disciplines that would not otherwise have been connected: math and philosophy. His influence was keenly felt no matter his actual contribution. For a review of the problems that resulted from a possibly overstated reputation of the Pythagoreans and the source materials, see Huffman. For more, see Cornford, Jaeger.
[viii] Leonid Zhmud claims that the Egyptians helped the Greeks with practical geometry, or “land measurement”, but they did not influence the ancient Greeks even as much as the ancients believed. Pythagoras would then perhaps be one of the Greeks who began the abstract study of arithmetic and number. S. Luria (in Zhmud) points out that the Egyptians did influence the Greeks; their influence was not vital; the proofs were the result of Greek genius. Walter Burkert adds to this perspective that the Greek study of mathematics was not Pythagorean, but Greek. He claims as well that the Pythagoreans would not have been amazed at their discoveries had they been actual mathematicians. Francis Cornford seems to have believed that Parmenides was influenced by the Pythagoreans, and there is some possibility that Parmenides was a former Pythagorean. Otto Neugebauer agrees that the “Pythagorean” theorem had been used for centuries in Babylon, but the Babylonians never evolved into scientific thinkers and Euclidean mathematics and axiomatic methods were exclusively Greek developments. For an ancient account of the Pythagorean discovery of musical intervals, see Boethius De Institutione Musica I, chaps. 10-11.
[ix] The interval sounds are in the plucking of an open string. It is the depression of the string at the correct place that brings out the sound. All musicians of Pythagoras's time would have known the phenomenon. For a succinct and clear explanation of how the intervals operate, see Ferguson. Van der Waerden thinks that Pythagoras himself ought to be credited with the mathematical understanding of the harmonic ratios, which were already known. Van der Waerden also thinks that Pythagoras ought to be credited with understanding that sound comes from vibrations in air.
[x] Whitehead claims that Pythagoras began a long tradition of examining the importance of definite numbers in the make-up of the world and even of god. Yet, J.A. Philip points out that there is no evidence for mathematical advancement among the Pythagoreans before Archcytas, a student of Pythagoras. For more, see Maziarz and Greenwood.
[xi] There are other ways to interpret this insight. Some critics say that Pythagoras and his followers thought of numbers as extended things and not as ratios, for instance. J.A. Philip claims that the harmonia of the one is the balance of odd and even and thus the “number-thing” of what something is is this balance. For an explication of the limit and unlimited, see Maziarz and Greenwood,
[xii] Proclus claims that the Pythagoreans claimed the “how many” subsists in itself or must be related to another, and the “how much” or quantity moves or remains in place. Thus Pythagoreans asserted that math arithmetic is the quantity that subsists itself, but music is related to another and geometry understands continued quantity in so much as it is not moveable, Proclus in Friedlein, p. 35. Marziarz and Greenwood claim the Babylonians taught Pythagoras that the constellations have two characteristics: amount of stars and shape of configuration. This concept and the ratio of the musical scale suggested number for everything, including ethics and religion. They also claim that the Pythagoreans attempted to find a deeper explanation of reality than Milesians like Thales. Numbers were stripped of particulars and thus “could be taken as the real constituents...of the world.” 14 It is notable that the Pythagoreans most likely did not agree among themselves.
[xiii] See Plutarch (Diels, Dox. 96), Stob. Ecl. Phys. I.I. 10, p22 in Cornford (1923).
[xiv] There are also ten vertices in the five-pointed Pythagorean star and ten pairs of opposites (principles): limit/ unlimited, odd/even, one/many, right/left, at rest/moving, straight/curved, square/oblong, light/darkness, male/female, good/bad. For a clear explanation of the Pythagorean use of the number ten, see Anglin.
[xv] We will see later that the Pythagoreans may have been quite shaken, and understandably so, when they discovered irrational numbers.
[xvi] George Allman correctly points out that “according to Plutarch, the Egyptians knew that a triangle whose sides consist of 3, 4, 5 parts, must be right-angled” 29. If the Egyptians were aware of the practical application of what we call the Pythagorean theorem, then Pythagoras perhaps made a proof of the theorem but he did not discover its mathematical truth. His not discovering this truth does not mean that he made no contribution, but his real contribution is perhaps less than has been estimated. Euclid's proof of the Pythagorean theorem is Euclid, I, 47. For an explication of a proof, see Maziarz and Greenwood.
[xvii] Aristotle Met. A5, 985b23.
[xviii]Aristotle Met. A5, 986b2.
[xix] Kirk and Raven point out that the unit (1) is indivisible and so the relationship between the odd and even numbers is visualized by the above gnomons. The unit in ¼ is a relationship of one unit out of a total of four. The unit would seem then to be divisible by repetitions of itself and thus be divisible, but only in a sense. The unit is preserved in the fraction while at once it is divided.
[xx] For more on the limit and unlimited, see Maziarz and Greenwood,
[xxi] See also Aristotle Met. M6, 1080b16.
[xxii] Kirk and Raven, The PreSocratic Philosophers, 246-50.
[xxiii] This conception may have been borrowed from Anaximander. For more on this fundament of the universe, see Cornford (1923).
[xxiv] There are later refinements of this kind of argument for the magnitude of numbers, some creating squares and then cubes. The end in any case is the same. It seems to have been argued that number is precisely what allows configurations of point, line, plane, solid to come about and so the kind of shape and then solid would not be as important, except that certain shapes were more important than others. The Pythagoreans were compelled to reconfigure their arguments after Parmenides' criticism of their association of number with objects. There are, thus, pre-Parmenidean and post Parmenidean Pythagoreans and such arguments are not necessarily post Parmenidean.
[xxv] Catherine Rowett points out that the Pythagoreans took the cosmology of Anaximander and applied mathematical ratio to it. Anaximander's ratios were arbitrary, but the Pythagoreans applied their notion of number in a much more logical manner. She claims that Pythagoreans appealed to “patterns of numbers” and worked out a more logical harmony of opposites than Heraclitus, and thus taking Heraclitus and Anaximander seriously, but not the Pythagoreans, is inconsistent and incorrect. See Burnett, Heath and Maziarz and Greenwood.
[xxvi] Aristotle, Physics IV.6, 213b22. Charles Kahn points out that the One is technically not a number, since it is prior to numbers; the numbers divide into odd and even, and the One itself is even and odd. This seeming paradox is part of the Pythagorean universe and itself may suggest why the Pythagoreans may not have had the crisis of irrational numbers thought so long by scholars to have taken place. For more on the cosmogony and the crisis, see Kahn and Zhmud.
[xxvii] No definitive proof exists, but some scholars show that the only evidence we have of deductive proof early in Greek history are the arguments of Parmenides and Zeno. The Pythagoreans did the same, perhaps. We do not know. For more, see Szabo.

THE PYTHAGOREANS BIBLIOGRAPHY:

Allman, George Johnston. 1976. Greek Geometry from Thales to Euclid. New York.
Anglin, W.S. 1994. Mathematics: A Concise History and Philosophy. Nerw York, Berlin.
Barker, Andrew. 1994. “Ptolemy's Pythagoreans, Archytas, and Plato's Conception of Mathematics.”Phronesis 39, No. 2: 113-135.
Beatty, H. 1914. “The Pythagoreans,” Hermathena 18, No. 40: 158-174.
Booth, N.B. 1957. “Were Zeno's Arguments Directed against the Pythagoreans?” Phronesis 2, No. 2: 90-103.
Borroff, Edith. 1978. “Ancient Acoustical Theory and a Pre-Pythagorean Comma.” College Music Symposium 18, No. 2: 20-23.
Burnett, J. 1930. Early Greek Philosophy, 4th ed. London.
Burnyeat, M.F. 1962. “Time and Pythagorean Religion.” The Classical Quarterly 12, No. 2: 248- 251.
Cornford, F.M. 1922. “Mysticism and Science in the Pythagorean Tradition,” The Classical Quarterly, 16, No. 3/4: 137-150.
____________. 1923. “Mysticism and Science in the Pythagorean Tradition (Continued),” The Classical Quarterly, 17, No. 1: 1-12.
____________. 1952. Principium sapientiae: The Origins of Greek Philosophical Thought. Cambridge.
Crocker, Richard L. 1963. “Pythagorean Mathematics and Music.” The Journal of Aesthetics and Art Criticism 22, No. 2: 189-198.
Diemel, R.F., Hersey, Mayo D. 1911. “The Pythagorean Theorem.” Science, New Series 33, No. 847: 457.
English, Robert B. 1912. “Parmenides' Indebtedness to the Pythagoreans.” Transactions and Proceedings of the American Philological Association 43: 81-94.
Ferguson, Kitty. 2008. The Music of Pythagoras: How an Ancient Brotherhood cracked the Code of the Universe and Lit the Path from Antiquity to Outer Space. New York.
Friedlein, Godofredi. 1873. Primum Euclidis Elementorum Commentarii. Leipzig.
Heath, Thomas. 1921. A History of Greek Mathematics, I. New York.
Heidel, W.A. 1940. “The Pythagoreans and Greek Mathematics.” The American Journal of Philology 61, No. 1: 1-33.
Huffman, C. 1999. “The Pythagorean tradition,” in A.A. Long (ed.), The Cambridge Companion to Early Greek Philosophy. Cambridge.
Kadison, Richard V. 2002. “The Pythagorean Theorem: I. The Finite Case.” Proceedings of the National Academy of Sciences of the United States of America 99, No. 7: 4178-4184.
Kahn, Charles. 2001. Pythagoras and the Pythagoreans, a brief History. Indianapolis/ Cambridge.
Levy, Ernst. 1945. “Pythagorean Bases for a New Investigation of Harmony.” Bulletin of the American Musicological Society, No. 8: 5.
Lloyd, Geoffrey. 2014. “Pythagoras,” in A History of Pythagoreanism Carl A. Huffman ed. Cambridge.
Luria, S. 1933. “On the Problem of Egyptian Influences on Greek Geometry,” Archive of the History of Science and Technology.
Macfarlane, Alexander. 1911. “The Pythagorean Theorem.” Science, New Series 34, No. 867: 181-182.
Marantz, Samuel A. 1967. “Integral Solutions to the Pythagorean Formula.” The Science Teacher 34, No. 5: 68, 70.
Maziarz, Edward and Greenwood, Thomas. 1968. Greek Mathematical Philosophy. New York.
Miller, John F. 1979. “Time as the Soul of the World: A Meditation on the Pythagorean Conception of Time,” Apeiron: A Journal for Ancient Philosophy and Science 13, No. 2: 116-123.
Netz, Reviel. 2014. “The problem of Pythagorean mathematics,” in A History of Pythagoreanism. Carl A. Huffman ed. Cambridge.
Neugebauer, Otto. 1957. The Exact Sciences in Antiquity. New York.
Northrup, Edwin F. 1910. “Is this a Dynamical Proof of the Pythagorean Theorem?” Science, New Series 32, No. 833: 863-864.
Philip, J.A. 1966. “The 'Pythagorean' Theory of the Derivation of Magnitudes.” Phoenix 20, No. 1: 32-50.
________. 1963. “Aristotle's Monograph on the Pythagoreans.” Transactions and Proceedings of the American Philological Association 94: 185-198.
________. 1963. “Aristotle's Sources for Pythagorean Doctrine.” Phoenix 17, No. 4: 251-265.
________. 1968. Pythagoras and Early Pythagoreanism. Toronto.
Prowse, K.R. 1964. “Numa and the Pythagoreans: A Curious Incident.” Greece & Rome 11, No. 1: 36-42.
Rowett, Catherine. 2013. “Philosophy's Numerical Turn: Why the Pythagoreans' Interest in Numbers is Truly Awesome,” in Doctrine and Doxography: Studies on Heraclitus and Pythagoras. David Sider and Dirk Obbink eds. Berlin, Boston.
Stahl, William H. 1942. “Pythagoras and Musical Concords.” The Classical Weekly 36, No. 1: 5.
Szabo, A. 1964. “The Transformation of Mathematics into Deductive Science and the Beginnings of Its Foundation on Definitions and Axioms,” Scripta Mathematica 27, 27- 48, 113-39.
Taylor, A.E. 1926. “The Pythagorean Philosophemes.” The Classical Review 40, No. 5: 149- 151.
van der Waerden, B.L. 1943. “Harmonielehre der Pythagoreer,” Hermes 78, 163-199.
West, M.L. 1971. “Callimachus on the Pythagoreans.” The Classical Review 21, No. 3: 330-331.
Whitehead, A. N. 1941. Science and the Modern World. New York.