Archimedes
Life and Works
Archimedes was almost a modern scientist, though he lived from 287 to 212 B.C. He was born and lived in Syracuse, but he may have traveled to Alexandria Egypt in order to study geometry and mathematics. Archimedes was friend to king Hieron of Syracuse and perhaps his family was somehow connected to the royal household. Whatever his connection to royalty, Archimedes enjoyed wide latitude and freedom to pursue his interests. There are more than a few stories about him, and as usual these tales are suspect, but they point to what his life may have been. King Hieron asked him to determine if a crown made by a possibly unscrupulous blacksmith was constructed from pure gold. The king suspected another metal had been mixed into the crown and consecrating a gold and silver crown as gold would be an insult to the gods. Thus, the issue was spiritual and politically important. Archimedes is famous for the method by which he determined the composition of the crown as well as his reaction when he discovered the solution. Ancient sources claim that he was in a bath and he noticed that when his feet entered the water, he displaced a certain volume of the liquid. Without concerning himself to don clothing he ran from the bath naked, saying “I have found it” or Eureka in ancient Greek. Archimedes is said to have been killed during the capture of Syracuse by the Roman general Marcellus, who wanted Archimedes to be taken unharmed, but perhaps because of the eccentric mathematician's dismissive disposition he died at the hands of a soldier. There are conflicting anecdotes about his death. One is that a soldier came in order to fetch him for Marcellus and when Archimedes saw a shadow on the proof he currently worked, he demanded the soldier get out of his way. Another story [i] tells of how a soldier came to Archimedes who was so absorbed in his work that he had not noticed Syracuse had fallen to the Romans. The soldier said to Archimedes that Marcellus awaits and Archimedes replied that he wanted to finish his proof first. In either case, the soldier grew angry and slayed the septuagenarian mathematician. It is likely that we will never know precisely how Archimedes died, but he almost certainly perished in the taking of Syracuse.
Several works of Archimedes survive extant, but a new codex has recently come to light and perhaps more of his work awaits rediscovery. On the Sphere and Cylinder is the work he was most proud to create, including a calculation for the surface area of a sphere and that the volume of a sphere is two-thirds that of the cylinder in which it is inscribed. [ii] Measurement of the Circle is a section of a longer work that has in it a calculation of π, still a mathematical constant. On Conoids and Spheroids determines the volumes of segments of solids in a conic section, which is a precursor to calculus. On Spirals deals with tangents to and areas related to the spiral of Archimedes.[iii] On the Equilibrium of Planes [iv] concerns centers of gravity of various figures; it establishes the “law of the lever.” Quadrature of the Parabola asserts that the area of any segment of a parabola is 4/3 of the area of a triangle having the same base and height as that segment, among other things. The Sand Reckoner attempts to express very large numbers in an effort to remedy Greek numerical notation. Method Concerning Mechanical Theorems describes mathematical discovery, demonstrating how Archimedes used a “mechanical” method in some of his primary discoveries. On Floating Bodies concerns hydrostatics; it determines positions solids will take while floating in fluid. Archimedes wrote other works that do not survive, but what scholars possess is formidable indeed. One, called the Stomachion, is a game consisting of a square cut into fourteen pieces.
First Principles
Archimedes was an eccentric, seemingly interested only in his calculations and his not insignificant insights into material reality, and so his main preoccupation was pure mathematics. One may be justified in calling him a theoretical mathematician, except that the specific modern difference between theoretical and applied mathematics did not exist during his lifetime, and Archimedes used theoretical mathematics to make discoveries about empirical aspects of material reality; he used material reality for insights into mathematics. He, like modern physicists, used mathematics and geometry to explain the “how” of material reality. Archimedes explains the geometric aspects of the effect of gravity upon a lever in Equilibrium of Planes, for example. Occasionally, he paused from his work in order to invent some practical device. These practical devices are the things for which he was popularly known in the ancient world: the water screw, possibly a grappling hook that was a siege-engine of war, a method for determining the density of an object placed in water. Archimedes, like Euclid, does not explicitly state his first principles. Numbers for Archimedes seem to have a spatial significance, though he was likely not a Pythagorean in the traditional sense. He applies geometry to relations between physical objects and motions and in this sense his work anticipates what is called classical mechanics in physics. Archimedes' lack of application of applied mathematics tells us that he was not necessarily seeking god or the origin of the universe in his work, but rather he seems to be observing and working out mathematical observations and relationships of physical happenstance. He may be thought of as having a first principle of mathematics as it is applied to motion, objects and physical relationships. He studied what was there and sought regular patterns that could be explained upon each manifestation through numbers. Seemingly unconcerned to articulate first principles, he believed in the ability of mathematics to explain how things operate and that is a fundamental aspect of modern science.
Causation and Cosmology
Archimedes may have believed in a heliocentric universe, but we may correctly suspect that he did not believe in the traditional pagan gods in the manner that his contemporaries did. His Sand Reckoner contains what may be a clue to Archimedes' s cosmology: a description of a heliocentric system and an attempt to determine the sun's diameter. Causation for Archimedes seems to lie at least partially in gravitation as well as in differences between shapes of objects interacting with one another in space, and not necessarily time. Thus, explanation of how objects operate in the universe is a fundamental aspect of what may be called his cosmology, which is the same as saying that he is a precursor to those early modern physicists who defined and labored over classical mechanics, classical mechanics being the concern over the physical laws that make up motions of objects that have been influenced by forces of the universe. The study of motion was not new, even to Archimedes, but he studied motion without the hindrance of seeking god or the prejudice of a preconceived notion of some kind of transcendence. He simply sought to explain how what is there operates physically. One cannot call his perspective objectivity, but one may want to say that he carried with him less preconceived notions than earlier thinkers. He is an applied mathematician and geometrician. Thus, the mechanical objects he discovered and his breakthroughs in geometrical relationships are manifestations of his sense of causation and how the universe around us is composed. Thus, he does not articulate a cosmology, and if he did he would not have adhered to a traditional one, thought it may have had the veneer of traditional belief.
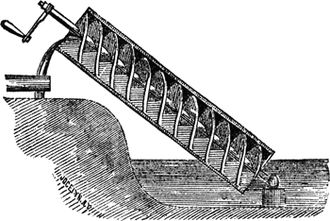
Archimedes' water screw [v] is a simple mechanism still employed to drive water up from depths where perhaps it otherwise may be impossible to obtain. The device is rather simple in construction. It is a tube with blades lining the inside in the shape of a screw.
As the tube turns it drives water up or down depending on the direction of the rotation. The tube can be stationary with the screw-blade inside moving or the apparatus can be constructed such that the whole of the tube moves and thus the position of the blades changes. In either case, the result is the raising or lowering of liquid. In some instances the screw is used for moving dirt or other material. Able to be constructed of any length and capable of relocating any kind of liquid, the device has myriad applications and remains in use today. It is a simple construction that makes use of geometric shapes to form an ergonomic device. If Archimedes did not design the water screw, then someone with a practical knowledge of geometry did. Another anecdote that speaks to Archimedes' talent for practical invention is the verifiable story of king Hieron II when he asked Archimedes to determine if a crown was genuinely constructed from solid gold or not. There is some debate as to how Archimedes evaluated the density of the crown, but it is likely he made use of his Law of Buoyancy [vi]:
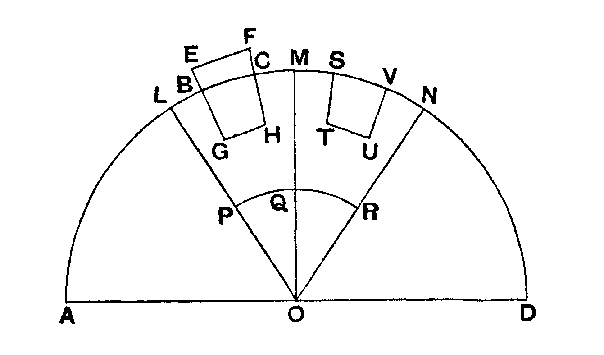
On Floating Bodies I, Proposition 5: Whatever solid is lighter than a fluid in magnitude will, once set in the fluid, be submerged in such a way that as much as is the weight of the solid, just so much is the weight of the submersion; let it have an equal heaviness to the whole magnitude. Let the same things be distributed, and let the fluid not move. Let the solid be EGHF, and let BGHC be the portion of it immersed when the fluid is at rest. Conceive a pyramid with vertex O including the solid, and another pyramid with the same vertex continuous with the former and equal to it. Suppose a portion of the fluid STUV at the base of the second pyramid to be equal and similar to the immersed portion of the solid; and let the construction be the same as in proposition 3. If therefore the fluid is not moved, similarly the parts of it itself placed inside are pressed equally.
Then, since the pressure on the parts of the fluid at PQ, QR must be equal in order that the fluid be at rest, it follows that the weight of the portion STUV of the fluid must be equal to the weight of the solid EGHF. And the former is equal to the weight of the fluid displaced by the immersed portion of the solid BGHC. It is clear then, that as much as is the weight of the fluid, so much is the part of the magnitude of the solid submerged and it has equal heaviness of the entire magnitude. and his Law of the Lever [vii]:
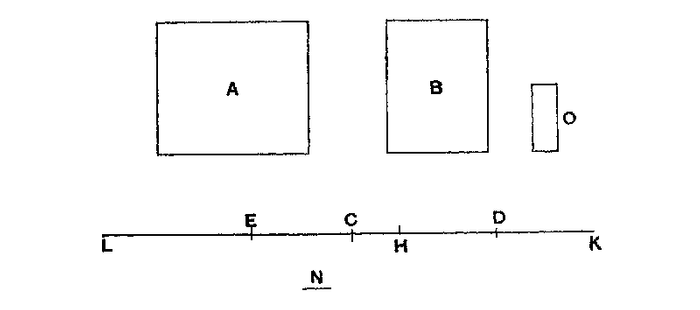
6: Commensurable magnitudes establish an equilibrium at lengths proportionally corresponding to the magnitudes. Let A, B be commensurable magnitudes, and let A, B be their centers. Let DE be a straight line divided at C so that as A is to B, so is DC to CE.
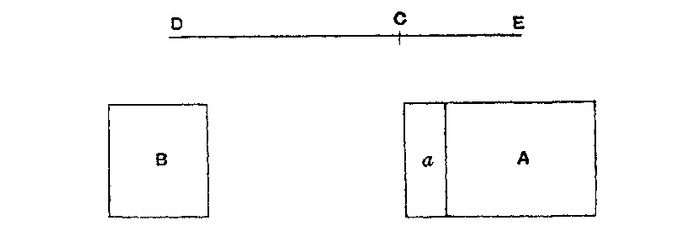
It must be shown that, if A is positioned at E and B at D, then C is the center of the two. Because A, B are commensurable, so are DC, CE. Let N be a common measure of DC, CE. Produce DH, DK each equal to CE, and EL (on CE) equal to CD. Then EH = CD, because DH = CE. Thus, LH is cut in half at E, as HK is cut in half at D. Then LH, HK must both contain N evenly. Let there be a magnitude O so that O is measured as many times in A as N is measured in LH, and from that as A is to O, so LH is to N. But as B is to A so is CE to DC and HK to LH. The result is, correspondingly, as B is to O, so is HK to N, or B is measured by O as much as HK is measured by N. Then, O is a common measure of A, B. Cut LH, HK into parts each equaling N, and cut A, B into parts each equaling O. The parts of A will equal those of LH in number, and the parts of B will be equal those of HK in number. Set one part of A at the middle of each of the parts N of LH. The center of the parts of A, placed equal distances on LH, will be at E, the middle point of LH [Prop. 5, Cor. 2], and the center of the parts of B, placed equal distances on HK, will be at D, which is the middle of HK. A is then applied at E and B applied at D. Yet the configuration formed by the parts O of A and B together is a configuration of equal magnitudes even in number and set at equal distances along LK. And because LE is equal to CD and EC is equal to DK, then LC is equal to CK so that C is the middle of LK. Therefore, C is the center of the configuration along LK and thus A operating at E and B operating at D balance around C. 7: Incommensurable magnitudes establish an equilibrium at lengths proportionally corresponding to the magnitudes. Let the magnitudes be incommensurable, and let them be (A + a) and B. Let DE be a straight line divided at C so that (A + a) as to B is equal to DC as to CE. If (A + a) positioned at E and B positioned at D do not balance around C, (A + a) is too large to balance B, or not large enough.
Let (A + a) be too large to balance B. Subtract from (A + a) a magnitude smaller than the subtraction that would make the remainder balance B, but so that the remainder A and the magnitude B are commensurable. Because A, B are commensurable and A to B is less than DC to CE, A and B will not balance [Prop. 6], but D will be depressed. But this is impossible, because a-subtracted was insufficient reduction of (A + a) to produce equilibrium; the result was that E remained depressed. Therefore, (A + a) is not too large to balance B; and likewise it may be proven that B is not too large to balance (A + a). The result is that (A + a), B together have their center at C.
One suspends the crown [viii], which amounted to a wreath made of supposed gold, on one end of a scale and balances it with an equal mass of gold on the other end. One immerses the crown and gold along with the apparatus into a container of water. If the crown and the gold balance on the scale while submerged, then the two have the same volume, and the crown has the same density as the gold. If the scale tilts toward the gold, then the crown has a greater volume and its density is less. The crown would then be an alloy of gold and some other, lighter metal. Scholars do not know precisely how Archimedes determined the weight and density of the crown, but it is likely that these two propositions were integral to solving the problem. If one understands the laws of proportions, even in a purely mathematical way, then one can see the affects of gravity upon physical objects clearly. As long as a geometric rendering of the physical interaction is possible, Archimedes was able to find it. In other words, the spatial relationship of the objects on the lever and in the water corresponds to the relationship of the weight of each object and that weight's affect on the other objects. A physical interaction can be reduced to a geometric formula and so pure math renders how material reality interacts. Here is a wholeheartedly modern method that discovers something empirically verifiable by purely mathematical means. As modern and incredible as these discoveries seem historically, they are practical inventions that were probably only afterthoughts on Archimedes' part, if one takes the surviving anecdotes as evidence of his attitude.
Argumentation
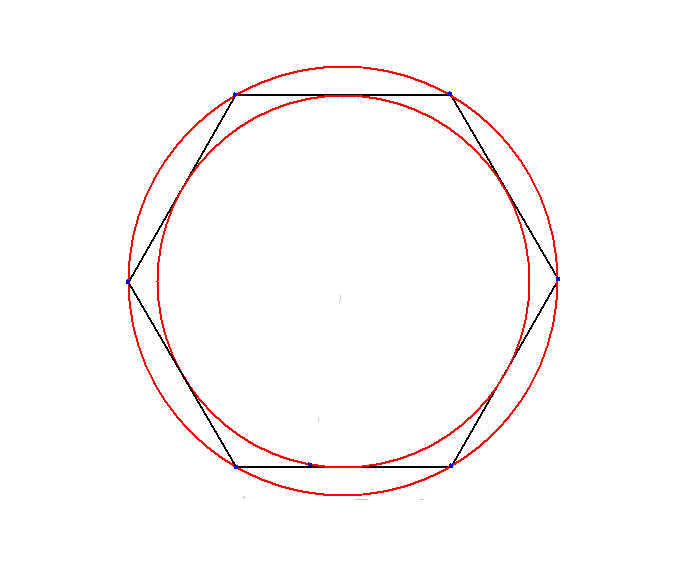
Other insights were much more theoretical, and to his liking. These were not known widely, but Archimedes shared them with like-minded thinkers. Thus, Archimedes also engaged in more pure mathematical exercises. For instance, he found a way to determine the value of π. π is a mathematical constant, the ratio of the circumference of a circle to its diameter. It is the same ratio no matter what the size of the circle and like the Pythagorean theorem it is true whether or not there exists some shape that has come into existence. It has been used by mathematicians to found many systems and proofs. Remember that Euclid needs axioms and postulates in order to begin arguing for a certain point. Aristotle's conversion, contraposition and obversion of different statements are the same logical conception. These are reliable truths that philosophers, logicians and mathematicians can employ as initial certainties, or at least givens. A sound proof, argument or proposition cannot exist without these foundations. Archimedes' method for determining the value of π is somewhat complicated, and so it is not included in this section, yet his basic idea is simple, possessing both mathematical and geometric aspects. He constructed a polygon consisting of equilateral triangles inside of a circle. He then constructed another polygon with the same number of sides outside of a circle. The polygons have six sides initially. The polygon inside of the circle is inscribed; the polygon outside the circle is circumscribed.
i Obtained from http://www.math.nyu.edu/~crorres/Archimedes/Crown/CrownIntro.html.
If we want to know how to calculate the relationship between the circumference and the diameter for the six-sided hexagon, then we divide the circumference by the diameter. Since Archimedes constructed the hexagons from equilateral triangles, the first calculation is simple. The diameter of the inscribed hexagon is two where the circumference is six. 6/2 = 3 is the first calculation of π, because it shows the relationship between the circumference and the diameter of the hexagon, but it is not very accurate because the hexagon merely resembles a circle. One needs a shape that is much closer to the circle in order to find the better approximation. One can simply measure the perimeter of the hexagon, but then the calculation is limited by one's tools, and π is an irrational number. So, 3 cannot be π. It is merely an approximation. Archimedes constructed another set of polygons, one inscribed in the circle and another circumscribing the circle. These new polygons were dodecagons, each possessing twelve equal sides. He thus doubled the number of sides of the polygons and they both now resemble more closely a circle.
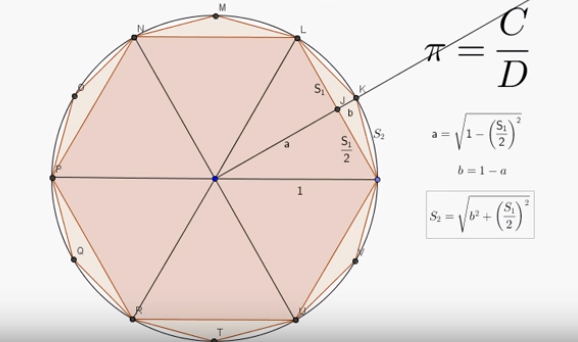
He then found the length of each new side, the sides being equal for each polygon, and when he multiplied the new length of each side by the number of sides of the new polygon he arrived at a number he was able to divide by the diameter of each shape in order to more closely approximate π. Yet, there remains a difficulty. Archimedes needed to know what the length of the new side was in order to calculate more accurately what the ratio is of the new figure. A more elegant and easier way to understand what Archimedes was doing is by using one polygon inside of a circle instead of his two. The Pythagorean theorem can then be used to determine the sides of the polygon. The inscribed polygon is the more elegant and more modern way of employing Archimedes' method. It works just as well, and it is easier to use. Remember that Archimedes used the calculations of triangles inside and outside the circle. He employed parts of Euclid's Elements as well as aspects of the Pythagorean theorem. The method below is a refined version of his method. One can say that it is derivative of Archimedes' method.[ix]
The first triangle one can determine because one knows the lengths of the two sides. The triangle is equilateral, so the sides are all the same length. The sides near the circle are cut in half (here in the upper right corner of the image), so if the diameter of the circle is 1, then each one of those sides is ½. We know by the Pythagorean theorem that a = √1- (S₁/2)² and b = 1 – a. We can see that S₂ = √b² + (S₁/2)². The Pythagorean theorem one can use to find the value of a and from that the value of b. Once the value of b is attained, the value of S₂ follows because we again use the Pythagorean theorem to determine its length. S₂ is the length of the side that we need. S₂ is multiplied by the number of sides in order to attain the perimeter, which is then divided by 2. 2 is the diameter of both the circle and the hexagon. Thus, a continually refined value of π can be found by increasing the number of sides until the sides of the polygon resemble more closely a circle. Archimedes was thus able to calculate the ratio of the circumference to the diameter each successive time he added sides to the figures inside and outside of the circle. He performed this same task repeatedly, each time bisecting the sides of the new polygon until he created a 96-sided figure. The 96-sided figure was a much closer approximation of the value of π because Archimedes used an accepted practice of exhausting the space between the figure whose sides he could determine and and the shape of the circle. In other words, the more sides created on a polygon, the more circular the polygon becomes. His astounding task was to find measurements of curved objects. Remember that ancient Greeks were able to determine the areas of things with triangles, but triangles do not fit neatly into curved shapes. Archimedes refines the method of exhaustion of Eudoxus.
One exhausts the space between the two shapes. Using two polygons, Archimedes approximated π to between two numbers: < 3 1/7 and > 3 10/71. That is why one polygon circumscribes the circle and another is inscribed. One must remember that π is a constant, but it is also an irrational number. Its calculation will continue indefinitely, if one continues to seek greater accuracy. Irrational numbers are strange in that they seem to exist as both odd and even numbers. They are like points on a line that can never be found and yet they are present. So, calculating π to its exact measure is not possible, but Archimedes approximated it with only a circle and a polygon of 96 sides. Archimedes' calculation of π is another example where math allows the thinker to make a determination of something that would not be possible merely with human senses. Math thus reaches into a part of reality where perception goes dark. One will remember as well that the Pythagorean theorem is an integral part of scientific development. It is useful in determining π with Archimedes' method. Not only does it tell us something about most triangles, but it is a constant, like π, that can be used in other proofs and it has practical applications. Again, when one is attempting to determine what the side of a new polygon is, one is able to use the Pythagorean theorem to determine its length because one knows the lengths of the other two sides of a right-angled triangle that is inscribed within the polygon. Again, one must keep in mind that Archimedes used two polygons, one inscribed in and one circumscribing the circle.
Archimedes, like any good mathematician, takes things that he knows, like constants and formulas taken from other mathematicians, and he uses them to find the things that he does not know. These inferences are really no different fundamentally than the ones of earlier mathematicians and philosophers, except they are geometrically or mathematically based rather than language based. The spirit of science resides in all of these insights and arguments about material reality. Archimedes' use of the Pythagorean theorem is only one such example. As we have seen, he also determined the area of a circle, πr² , which the ancients called squaring the circle. Euclid knew that there was some constant that allowed one to determine the area of a circle, but he did not know nor calculate what that constant was. When the value of π was found, the calculation became possible. One may recall the discussion earlier in this text about sine, cosine and tangent. These are all mathematical constants used in calculating formulas and proofs. They are aspects of triangles themselves, like the Pythagorean theorem. One may also recall Plato's eidos, which is a kind of constant ideal in which something participates. These geometric formulas are similar to a Platonic eidos in that they are constant calculations that will exist for each triangle or circle or whatever shape, no matter whether there is a manifestation of them or not. In that sense modern science is built on something that closely resembles a Platonic form, or eidos. Scientists may not want to admit to being Platonists, but some fundamental aspects of their very way of arguing relies upon notions that inspired Plato's theory of eidos.
Endnotes
- i Plutarch's Parallel Lives: Marcellus.
- ii Archimedes requested that a representation of this discovery be placed on his tomb, which it was.
- iii The locus of a point moving with uniform speed along a straight line that itself is rotating with uniform speed about a fixed point. (You found this precise phrase here: https://www.britannica.com/biography/Archimedes)
- iv Scholars suspect that much of this book is a spurious creation of Archimedes, as it contains reworkings below the standard of Archimedes. Perhaps its main concept was conceived by thinkers who came before Archimedes.
- v Some scholars believe that Archimedes did not invent the water screw. It is supposed that he perhaps refined the design on a trip to Egypt or that others, amazed at his ability to construct workable devices, attributed it to him mistakenly. Perhaps Archimedes was merely alive at the time the screw was introduced to the Greeks and he was given credit for its invention because of his fame. For more, see Oleson, John Peter (1984), Greek and Roman Mechanical Water-lifting devices. The History of Technology, Dordecht: D. Reidel.
- vi Parts of this translation were taken from Heath, Thomas. 1897. The Works of Archimedes. Cambridge, Cambridge University Press. The section is On Floating Bodies.
- vii Portions of this translation were taken from the above text. The section is Equilibrium of Planes.
- viii Obtained from http://www.math.nyu.edu/~crorres/Archimedes/Crown/CrownIntro.html.
- ix One can watch a working out of p here: https://www.youtube.com/watch?v=_rJdkhlWZVQ
ARCHIMEDES BIBLIOGRAPHY:
- Apostol Tom M. and Mnatsakanian, Mamikon A. 2004. “A Fresh Look at the Method of Archimedes”, The American Mathematical Monthly 111, No. 6: 496-508.
- Berggren, J.L. 1976. “Spurious Theorems in Archimedes' Equilibrium of Planes: Book I”, Archive for History of Exact Sciences 16, No. 2: 87-103.
- Boyer, B. 1945. “Quantitative Science without Measurement: The Physics of Aristotle and Archimedes”, The Scientific Monthly 60, No. 5: 358-364.
- Bromwich, T.J.I'a. 1928. “The Methods Used by Archimedes for Approximating to Square- Roots”, The Mathematical Gazette 14, No. 197: 253-257.
- Brown, Ezra. 2004. “The Ancient World's Magical Genius Thinks BIG”, Math Horizons 12, No. 2: 5-8.
- Dehn, Max. 1944. “Mathematics, 300 B.C.--200 B.C.” The American Mathematical Monthly 51, No. 1: 25-31.
- Del Grande, John. 1993. “The “Method” of Archimedes”, The Mathematics Teacher 86, No. 3: 240-243.
- Eagle, Ruth. 1998. “A Typical Slice”, Mathematics in School 27, No. 4: 37-39.
- Ehrlich, Philip. 1997. “From Completeness to Archimedean Completenes: An Essay in the Foundations of Euclidean Geometry”, Synthese 110, No. 1: A Symposium of David Hilbert: 57-76.
- Evans, George W. 1927. “A Riddle from Archimedes”, The Mathematics Teacher 20, No. 5: 243-252.
- Fletcher, C.R. 1972. “More on Archimedes”, Mathematics in School 1, No. 5: 11.
- Gardies, Jean Louis. 2003. “Do Mathematical Constructions Escape Logic?”, Synthese 134, No. 1/ 2 Logic and Mathematical Reasoning: 3-24.
- Helmer, Olaf. 1935. “On the Theory of Axiom-Systems”, Analysis 3, No. 1/ 3: 1-11.
- Kalman, Dan. 2007. “Archimedes in the 5th Dimension”, Math Horizons 15, No. 2: 8-10.
- Kane, R. 1986. “Principles of Reason”, Erkenntnis 24, No. 2: 115-136.
- Kaplan, Gail. 2003. “MATH ROOTS: EUREKA! Or Don't Throw out the Crown with the Bathwater”, Mathematics Teaching in the Middle School 8, No. 9: 484-488.
- Kasner, Edward. 1933. “Squaring the Circle”, The Scientific Monthly 37, No. 1: 67-71.
- Knoff, Wilbur R. 1976. “Archimedes and the Measurement of the Circle: A New Interpretation”, Archive for History of Exact Sciences 15, No. 2: 115-140.
- Lange, Les. 1994. “Archimedes”, The Mathematics Teacher 87, No. 2: 68.
- Lorenzen, Paul. 1960. “Constructive and Axiomatic Mathematics”, Synthese 12, No. 1: 114-119.
- Miller, G.A. 1928. “Archimedes and Trigonometry”, Science: New Series 67, No. 1744: 555.
- Netz, Reviel. 2003. “The Goal of Archimedes' "Sand-Reckoner"”, Apeiron: A Journal for Ancient Philosophy and Science 36, No. 4: 251-290.
- Pixley, Loren W. 1965. “Archimedes”, The Mathematics Teacher 58, No. 7: 534-636.
- Robinson, Richard. 1936. “Analysis in Greek Geometry”, Mind 45, No. 180: 464-473.
- Shilgalis, Thomas W. 1989. “Archimedes and Pi”, The Mathematics Teacher 82, No. 3: 204-206.
- Sigma Xi. 1999. “Archimedes Unbound”, American Scientist 87, No. 4: 316-318. .
- Simms, D.L. 1990. “The Trial for Archimedes's Tomb”, Journal of the Warburg and Courtauld Institutes 53: 281-286.
- Slowbe, Jason. 2007. “Pi Filling, Archimedes Style”, The Mathematics Teacher 100, No. 7: 485- 489.
- Society for Science and the Public. 1928. “Classics of Science: Weight in Air and Water”, The Science News-Letter 13, No. 368: 269-270.
- ____________________________. 1927. “True Story of Archimedes”, The Science News- Letter 12, No. 335: 169-170.
- Stein, Howard. 1990. “Eudoxos and Dedekind: On the Ancient Greek Theory of Ratios and Its Relation to Modern Mathematics”, Synthese 84, No. 2: 163-211.
- Vincent, S.P. 2007. “91.18 Archimedes Revisited: The Approximation of π by Regular Polygon Perimeters”, The Mathematical Gazette 91, No. 520: 117-120.
- White, Michael J. 1982. “Zeno's Arrow, Divisible Infinitesimals, and Chrysippus”, Phronesis 27, No. 3: 239-254.
- _____________. 2006. “On Doubling the Cube: Mechanics and Conics”, Apeiron: A Journal for Ancient Philosophy and Science 39, No. 3: 201-219.