Aristotle
Life and Works
Aristotle was a student of Plato who lived from 384 to 322 BC. He was arguably the most scientific of ancient thinkers, but not because he followed scientific methods. Aristotle developed a system of analysis based upon his metaphysics, employing some aspects of what would eventually give rise to scientific method. Having traveled to Pella in 343 B.C., he began tutoring Philip of Macedon's son, Alexander, who later came to be Alexander the great. He founded his own school at Athens in 334/335 B.C., called the Lyceum, where he enlisted the aid of students in making observations of practically everything that exists. His students were known as peripatetics, and he had with Herpyllus (a slave or his wife) a son named Nicomachus, to whom his Nicomachean Ethics is allegedly addressed. He felt compelled to depart Athens because of anti-Macedonian sentiment, which arose shortly after Alexander's death in 323 B.C., leaving Athens for Chalcis where he died of natural causes. His and his students' investigations supplied the raw material for many of his “scientific” works. Some that survive are Physics, Metaphysics, On the Heavens, On Generation and Corruption, On the Parts of Animals, Categories, Topics, On the Soul, Posterior Analytics, Prior Analytics, Nicomachean Ethics and Meteorologia. The topics of his surviving works range from biology to metaphysics, but many or even all of these are works that likely were not meant for publication. Indeed, the works that were meant to be read seem to have been lost, including some dialogues on Homer and poetry in general, which were said to be even more beautiful than the works of Plato. The breadth and depth of his thought continues to impress scholars [i] and some consider Aristotle to be the greatest polymath of the ancient world. Aristotle's metaphysics leads him to observe and thus to analyze empirically physical objects themselves instead of merely reasoning about them. As a result he created an empirical and logical system of thought that covered not only all of the humanities but all of what moderns call the hard sciences. In fact, Aristotle's contribution to western thinking is so immense that we must limit ourselves to only a few facets of his thinking and a few texts. [ii] Aristotle did not discover causality or causes. Rather, as we have seen, many thinkers before him sought causes of things in nature. These were the first physicists from the western world who had remarkable insights into material reality and who many times expressed themselves in literary form. Aristotle believed in a form of interaction with these predecessors that was similar to the dialogue form Plato used in his dialogues. He critiques his predecessors' work by discussing and critiquing their arguments and thus builds upon earlier insights, but in prose style.
First Principles
It is difficult to discern what comprises a first principle for Aristotle. His first principles can be thought to be a construct of things: elements, causes, motion and a material eidos. [iii] He was the first to create independent sciences and disciplines for various subjects and that is only one reason why articulating his first principle(s) is difficult. Aristotle was heavily influenced by Plato and so Plato's eidos is an intimate part of his thinking. Yet, Aristotle shifts the Platonic eidos from the immaterial reality of Plato to the material realm. [iv] He claims that the matter making up the manifestation of some creature or thing and the form, or eidos, are inextricably bound. Still, he retains the Platonic eidos as part of a metaphysical construct of things that move internally and externally and so become. This metaphysical eidos Aristotle then bound up with matter and motion. In other words, Aristotle thought that something has a nature if it moves into its own principle by becoming what it is:
Of existing things, some exist by nature, others through other causes: by nature animals and their parts exist, and plants, and the simple bodies, like earth, fire, air and water (for these things and things of this sort we say exist by nature), and all of these things seem to differ from the things not put together by nature. For each of these in itself possesses a source of movement and rest, in place or by growth and decrease, or by change; but a bed or a cloak, and other sort of thing that exists, by the manner in which it has happened upon each designation and to the extent that it exists from art, has no in-grown impulse of alteration at all. But by the manner in which they happen to exist of stone or earth or a mixture of these, they possess an impulse, and to that extent, since nature is a source of something and a cause of being moved and of being at rest in that to which it belongs principally, in virtue of itself and not accidentally, <they possess an impulse>. (Aristotle, Physics II, 192b8)
What he meant was that things that grow in and of themselves have a natural movement that can be likened to a particular principle, while things that must be crafted do not have this natural movement and thus no natures. A tiger has a nature, possessing an innate impulse to strive and survive as a tiger, as does a human. Beds and tables possess no nature because they have been crafted by someone; they lack the impulse to come about on their own. Yet, beds and tables exist by nature because they are crafted of things and made by men. Still, what comprises the table may have a nature or be a nature, depending on out of what the table is composed. In this manner Aristotle's perspective differs from Plato who thought that practically anything has an eidos, or what might be thought of as something like a nature, or some kind of organization. It is important to note that Aristotle deliberately avoids making a material element one of his first principles; he consciously avoids making a Platonic eidos a first principle as well, seemingly because he believed that any material principle or metaphysical construct would itself need another piece of matter or principle which would in turn need another first principle. There is then for Aristotle an infinite regress called the third man argument. Aristotle also acknowledged the four elements of Empedocles (earth, air, fire and water), but their status as first principles was for Aristotle dubious and they were not the principle he sought (again one significant reason is because of the third man argument). Some scholars claim that Aristotle argued himself into what is called prime matter, an underlying indefinite pure potentiality that inhered in the largest as well as the smallest and most fundamental of things.
It seems that Aristotle set out to explain how creatures and things arise in the world and what exactly is the relationship between the form, or organization, of something and its matter. Explaining matter and form as becoming in terms of potency and act seems to have been central to Aristotle's effort at understanding what it is that is the motion of a thing. Things that have an internal movement must be more than merely arrangements of the fundamental matter that comprises them. Otherwise, anyone could arrange matter in the correct way and create anything, god or creature. Aristotle sought what it is in matter that is yet more than mere material – that which produces itself, things and creatures yet remains en-mattered. In other words, he sought the things responsible for what comes to be, but these motions are not the mechanical activities modern science understands as causes. Aristotle set about to deepen human comprehension of the universe through investigation into productive activities that he called aitia, the Greek term meaning “causes.” Causes and things had different kinds of motion to them:
...there is motion only in respect of what kind, how much, and where, for in each of these there is contrary. Now let motion in respect of what kind be alteration, for it has been joined with this common name. But I say the what kind is not the thing in the substance of any thing (since then even the difference is a quality), but it is a passive attribute by which a thing is said to be affected or unaffected. Motion in respect of how much lacks a common name, but in each instance it is growth and decrease, the one tending to a thing's complete magnitude is growth, the other tending from it decrease. Motion in respect of place both in common and in particular is nameless, but let it be called generally change of place, although those things alone are said to be carried along when not on their own coming to a stand is possible for those things changing place. (Aristotle, Physics V, 3 226a).
This motion was intimately involved in what something is and how it manifests:
There is that which exists in completion, but also that which exists in completion and potentially: a thing being this thing, being this much, being this kind, or similarly for the other ways of categorizing being. Relation to something is said to be what exceeds or falls short, or what exists according to acts and being acted upon, and generally what moves (another thing) and what is moved: for the mover is a mover of something moved, and the moved is moved by something moving it, and no motion exists besides [this] in things. For what changes always changes either in substance, or in quantity, or in quality, or in place, and there is no commonality to take from these...and with respect to which is neither...a this, nor a this much, nor a what kind, nor any other kind of being: so that neither motion nor change will be anything apart from the things mentioned, since there exists nothing besides the things mentioned. (Aristotle Physics III, 1).
The word for motion that Aristotle uses is kinesis. He links kinesis to energeia, a term used to express the being-at-work [v] that is the continued actualization and also potential:
With a distinction having come about according to each kind of being between the complete and the potential, the completion of a thing existing by potential – by the manner in which this sort of thing exists – is motion: of the alterable, qua alterable, it is alteration; of the grow-able and its opposite, what can decrease (no name is common to the two), it is increase and decrease, of the generable and destructible it is coming to be and passing away, and of the mobile as far as place it is change of place. (Aristotle Physics, III, 1).
Kinesis of something for Aristotle is a kind of activity belonging to a thing that makes what the thing is a what. In other words, something coming to be moves into what it is, as itself being acted upon and acting in various ways:
And that this is motion, is clear from the following. For whenever the buildable – by which we say this sort of thing exists as itself – exists completely, it is being built, and this thing is building. Similarly learning, healing, rolling, leaping, ripening, aging. And because some of the same things exist potentially and completely, not at the same time or not according to the same thing, but like something fully hot and potentially cold. Many things will act and be acted upon by each other; for in every case they will be act-able and able to be-acted-upon. The result is that the moving is naturally moved, since each such thing moves the thing being moved and itself. (Aristotle, Physics III, 1).
A thing also moves from itself and into itself as it continues its being-at-work. It is necessary to understand that the energeia or the being-at-work of something is for Aristotle the moving organization that is its being, that being which for Plato is called an eidos. Aristotle contends that such activity is in the world as something material: being-at-work. It is not in another, allegedly deeper and immaterial part of reality, as for Plato. That activity has its own motion into itself, but it also may exist as potential for another thing. As a result, things have in and as themselves a kind of potential, for Aristotle. They possess motions that not only make them what they are, but make them possibly other things, and they are not necessarily always the same motion:
But the fullness of what exists potentially, whenever existing completely and working, not as itself but just as movable, is motion. I mean by “just as” the following. Bronze is a statue potentially, but similarly it is not the fulfillment of bronze by which it is bronze that is motion. For it is not the same thing to exist as bronze and to exist as some potentiality, since if they were the same thing simply and by definition, the completion of bronze as bronze would have been motion. But they are not the same, as has been stated. This is clear in contraries. For to be potentially healthy and to be potentially ill are different, since being healthy and being ill would be the same thing. The underlying thing both being sick and being healthy, whether humour or blood, is one and the same. Since they are not the same thing, just as color is not the same as being visible, the fulfillment of the potential, as potential, is motion. (Aristotle, Physics III, 1).
Causation and Cosmology
Aristotle understood causality as the thing (that material eidos) acting in and for itself, and thus his metaphysics, along with the third man argument seen above, compelled him to refrain from establishing a simple, material first principle. [vi] In other words, Aristotle establishes four causes in order that observations of particular causality may lead to a deeper understanding of a manifestation of anything. When one articulates the causes, the depth of the what of any thing emerges:
For since our labor is for the sake of knowing, and we think we do not thus far know each thing until we have taken hold of the why of each thing (and this is the taking up of the first cause), it is clear that we must do this about both coming to be and passing away and about all natural change, so that, once we know sources, we may try to lead back to them each of the things that are sought. (Aristotle, Physics II, 3).
Aristotle's analysis is not restricted to matter or to empirically verifiable aspects of things, and in this sense his method does not resemble scientific method. That is, a cause may be the skill or knowledge someone has or the arrangement of something and its purpose, which differs greatly from the sort of cause associated with modern science. His perspective on causes one may call metaphysics. One Aristotelian cause is the material that comprises a something. It is something without which the movement, or nature, cannot manifest.
One manner of cause is said to be, then, that out of which something comes into being, while being an underlying presence in it, as bronze of a statue or silver of a bowl, and other kinds of these things. (Aristotle, Physics II, 3).
The bronze of a statue is a kind of material from which a statue may be made. There are other substances from which a statue can be made, of course, but they must have certain qualities: resilience, aesthetic beauty in themselves and perhaps the ability to melt, or at least the ability to be formed into some shape or organization. One way to understand matter here is that it is a kind of being-at-work itself that possesses another characteristic of potential as well. The continued whatness of bronze does not change but the motion of the potential for being statue acts through its being-at-work. Matter may be interpreted here as another being-at-work, or a mysterious part of the universe that cannot be articulated; there is also prime matter, which has been interpreted to be an indeterminate mass of pure potentiality. [vii] Another of Aristotle's causes has been called the formal cause. It is the organization of what something is or the what.
In another manner [cause] is the form (eidos) or pattern, and this is the reasoning of the “to be what it is”, and the kinds of this thing (as of the two-to-one ratio octave, and broadly number), and the parts that are in the reasoning. (Aristotle, Physics II, 3).
One will recall that the octave is the two-to-one numeric ratio applied by Pythagoreans to the lengths on a musical scale. Certain distances on one chord produce similar sounds. Without the specific distance of the chords and without the particular material in specific arrangement comprising a string that produces a musical sound there would be no similarity of vibration that produces a sound. Each thing that is necessary to produce the sounds in the length relationship of two-to-one or one-half is itself an arrangement needed to form the octave. These differing but harmonized arrangements are the producers of the octave and thus formal causes, or formal producing activities. Thus, there is a relationship and order to the formal cause and it has an arrangement to it, but [viii] Aristotle is not making the formal cause numeric in nature, as we have seen, other than to state that there is an organization, which may in turn be analyzed mathematically or logically. [ix] A thing's nature has a kind of activity that produces a fullness, one that the assessment of its eidos by mathematicians lacks. The fullness is articulated for Aristotle in its motion. One can see aspects of the modern conception of geometry and calculation as abstractions that must be proven here. Aristotle thinks of geometry as not numbers spatially extended, but as the outline of things that must be filled. What fills it is motion of a specific kind. So, a natural thing in movement is the fullness of something actually moving as itself. [x] A third cause is what may be called the motive or the efficient cause:
...it is that from which the initial source of change or of rest is, as the legislator is a cause, or the father of a child, or broadly the making of what is being made, or the changing of a thing being changed. (Aristotle, Physics II, 3).
The motive cause is similar to the modern notion of cause, as that which produces or acts upon another thing in the first place. There is a generative quality to this cause as in all Aristotelian causes, but the motive, or sometimes-called efficient, cause may be more properly called the initial interaction between cause and caused or perhaps the physically active cause. It is the initial motion and interaction between things that makes up this cause in the sense that there are things causing and being caused externally at the beginning of change. The last cause, sometimes called the final cause, explains why something has come to exist, or its purpose. Its end is not necessarily to produce a human purpose for something, but to produce some kind of activity that can be defined as the end or goal of something:
...it (cause) is meant as an end. This is the “for the sake of which”, as health is of walking around. Why is he walking around? We say “so that he becomes healthy,” and in speaking in this manner we think to have given the cause. (Aristotle, Physics II, 3).
This cause, coupled with the formal cause, is more completely representative of the Platonic eidos. One may even think of the formal and final causes as the same but immersed in different acts of what becomes. When something attains its fullness, it attains such fullness as what it already was and what it was and is to become. Such is the final cause. One can think of human DNA as analogous. When matter goes into the design of the creature whose DNA guides it, the end goal is that pattern or organization that is the DNA, or the structure of what the creature will be. We call it genotype. The actual manifestation is the phenotype. The genotype and the phenotype are inextricably fused for Aristotle, not only in creatures and men, but in anything that possesses the impulse of nature. The final cause is that towards which the impulse of motion directs itself in order to become what it is by nature. The Platonic eidos is sometimes interpreted as an ideal, or as something to which to strive. The final cause is similar, but of course it is in the matter whereas the Platonic eidos is immaterial and “outside” of becoming. We must keep in mind that though we have seen roughly what are the causes for Aristotle, his work contradicts itself perhaps, or at least there is an effort to explain and then reexplain that makes his thoughts twist and turn on the page one reads. Perhaps it is the case that Aristotle recognized how fused together are these causes such that no one articulation suffices, but elements of each enter into different being-at-works:
For cause is spoken of in many ways, and of those of the same form, one prior and one later, as in [the cause] of health is the doctor and also the craftsman, and [the cause of] the octave [is] the double and also number, and always all-encompassing things as related to particular ones. (Aristotle, Physics II, 3).
And all of them, both those things said naturally and those said by chance, are some potential things and other things working , as of building a house, either the builder or the builder building. And similarly it will be articulated for what things the causes are causes for the things that have been said, as [cause] of this statue or a statue or generally an image, and of this bronze or of bronze or generally of material, and the same with the things having happened by chance. Further, these things weaving themselves together (and being woven) [with] those will be said, such as not Polycleitus nor a sculptor but the sculptor Polycleitus. (Aristotle, Physics II, 3).
Aristotle examined becoming and thus sought to understand Plato's eidos in terms of how things bring about things. He was compelled to accomplish this task by looking at the things around him and then reasoning. At the same time that he developed an observational method, and probably as a result, Aristotle noted that there exist rules for thinking. The effort at articulating the rules for logic seems to be linked to the effort at finding causes. At the same time, Aristotle's logic rules make clear how his predecessors reasoned and allowed future thinkers to analyze the arguments of the tradition, as seen in the arguments given above for ancient thinkers. These efforts at explaining things in terms of cause make Aristotle an authentically analytic thinker, which is to say that an essential aspect of his thinking is based upon observation and then later reasoning over the various observations of animals, of substances, of politics, and of other objects and creatures one finds in the universe. That he is analytic is not to say that he concentrates on logic and the rules of logic alone. Aristotle's metaphysics compel him to observe and then reason. One seeks to understand what the causes are, and so the eidoi, of a particular thing's motion. Observation and thought were already fundamental aspects of Greek thinking, but Aristotelian causes articulated precisely what to observe and how to reason in order to make sound arguments about the general aspects of each thing as it is being-at-work. It is for these reasons that we can call Aristotle a scientific thinker, but be careful to know that he is no scientist. He never would have thought that one first needs an hypothesis that was well-thought, a theory that was followed by empirical verification. While observation was an essential aspect of his thinking, the control methods and supposedly objective verification process of science were virtually unknown to him. In fact, Aristotle may not even have possessed any awareness of object reality in the scientific sense. The notion that there exists an objective state of things that may be assessed by reason and reached through the senses whereby an empirical verification of a theory may take place was not a part of his observational method at all. In fact, he would have been averse to empirical verification, other than the use of observations. Again, Aristotle observed and assessed through reason, but never did he or his students empirically verify an already-systematized theory. [xi]
Aristotle articulated his cosmology in various works, but the most complete actual cosmology was his De Caelo, or “On the Sky”, which was accepted as true for more than 18 centuries. There he articulated a world composed of the four elements: earth, air, fire and water. These naturally move up or down in a sublunary realm with fire being the most light and earth heaviest. Objects are composed of the different elements and they are imperfect because their elements are displaced, the natural places for the elements being where they tend to go. Fire ascends and earth drops, for example. Bodies move thus naturally and we have already seen how a natural motion is a part of all things. Stars and planets are more exalted bodies that move in circles and earth lies in the center of the universe with the celestial bodies circling it. The initial motion of bodies was begun by a prime mover that is itself desired [xii] by all the other bodies. The prime mover manifests itself in no way because otherwise it would be imperfect; celestial bodies are moved by the prime mover and the movement radiates downward into other spheres that surround earth; the matter that comprises the celestial sphere is the eternal aether. These spheres number 55, explaining and predicting the motions of the stars, as the celestial bodies were affixed to each of the spheres. The principles that govern the celestial sphere are not for Aristotle the same as the ones that govern the sublunary sphere. The celestial sphere and its occupants are eternal while the sublunary sphere, with its elements, are mortal. This universe has always existed because it is perfect, and it will always exist. Obviously, Aristotle made use of observations in creating this model. Aside from the fact that most of his assertions are wildly inaccurate, it is notable that his 55-sphere system did somewhat accurately predict celestial motions. Aristotle himself recognized the speculative nature of his musings and expressed hope that another, more informed, theory may emerge.
Argumentation
Keeping Aristotle's perspective in mind, we are able to re-articulate his rules of logic that we discussed in the first part of this blog. A re-articulation will make clear how his metaphysics, his logical rules and his analytic method work together. Aristotle noticed certain things about how human beings reasoned. He formulated the first rules for argumentation, guidelines for the formation of good reasoning. Good reasoning involves not only observations that are true, or what moderns may call facts. Observations must be understood such that they have a connection to one another, and the more certain the relationship between specific observations, the more firm foundation will be the thought about a specific topic. [xiii] Aristotle began with propositions, which are statements taken to be true. If there exists no connection between the propositions, then no conclusion can follow. But if there is a connection between the propositions, then new information and insight may follow:
If then one wants to prove syllogistically A of B, either as an attribute of it or as not an attribute of it, one must assert something of something else. If now A should be asserted of B, the proposition originally in question will have been assumed. But if A should be asserted of C, but C should not be asserted of anything, nor anything of it, nor anything else of A, no syllogism will be possible. For nothing necessarily follows from the assertion of some one thing concerning some other single thing. Thus we must take another premiss as well. If then A be asserted of something else, or something else of A, or something different of C, nothing prevents a syllogism being formed, but it will not be in relation to B through the premisses taken. Nor when C belongs to something else, and that to something else and so on, no connexion however being made with B, will a syllogism be possible concerning A in its relation to B. For in general we stated that no syllogism can establish the attribution of one thing to another, unless some middle term is taken, which is somehow related to each by way of predication. For the syllogism in general is made out of premisses, and a syllogism referring to this out of premisses with the same reference, and a syllogism relating this to that proceeds through premisses which relate this to that. But it is impossible to take a premiss in reference to B, if we neither affirm nor deny anything of it; or again to take a premiss relating A to B, if we take nothing common, but affirm or deny peculiar attributes of each. So we must take something midway between the two, which will connect the predications, if we are to have a syllogism relating this to that. If then we must take something common in relation to both, and this is possible in three ways (either by predicating A of C, and C of B, or C of both, or both of C), and these are the figures of which we have spoken, it is clear that every syllogism must be made in one or other of these figures. The argument is the same if several middle terms should be necessary to establish the relation to B; for the figure will be the same whether there is one middle term or many. (Aristotle, Prior Analytics I.23).[xiv]
If an argument has a good connection, it can be said to be valid. Yet, validity only means that there are statements possessing some set of things in common with one another and because of that commonality, one can make a new statement about them. This new statement is called an inference. It is information derived form the propositions one is using that was not present until the argument came about.
- All quadrupeds are wild animals.
- All tigers are quadrupeds.
- Thus, all tigers are wild animals.
This argument has good form, and so it is valid because if we accept that all quadrupeds are wild animals and that all tigers are quadrupeds, we can come to a reasonable conclusion that all tigers are wild animals because they share a set or category: quadrupeds. This commonality allows us to draw a new inference from information we already possessed. Yet, it may not be the case that all quadrupeds are wild animals, and thus the argument would not be true even though it makes proper connections. The information in the premises must say something true about the world. Here is the observation that one makes in order to form good, sound arguments. Recall some of the statements of earlier thinkers. These assertions may be true or not true, but many assertions of the early Greek physicists are mere observations that are taken as universals. That they are not universal, or perhaps even not true, is what seriously complicates an argument. One wants, of course, to make good inferences, so arguments must possess a commonality that allows good form, but the premises (observations) must also be true. If the argument has true premises and good form, then it is said to be sound. So, while validity in argumentation is necessary, soundness of argument is the true goal.
Aristotle talks of argumentation in terms of sets of things. Remember that he thought the eidos was in the material comprising something. An eidos in fact is a kind of general category of existing things that possesses a kinesis and an energeia. We have seen that these terms assist in explaining being-at-work or what-it-is-to-be [xv] for a thing, or its nature. So, when he observed things in nature, Aristotle was seeking the eidos of some particular thing, its four causes. He was looking not just for what mechanical cause made something happen, but he sought also the “why” and the arrangement of it. Thus, he looked for formal and final causes. [xvi] When he made observations about things, he was able to say of them that they always or never had certain characteristics or that some of them had and some had none of certain characteristics. He was looking for the part of something that made it was it is as well as that part of it that made it potential for becoming something else, or a part of something else. When there was a connection between two things, he was able to say something about the eidos of what he examined:
- All quadrupeds are land-based creatures.
- All Tigers are quadrupeds.
- All Tigers are land-based creatures.
All of the set of quadrupeds belongs to the set of land-based creatures. So, nothing that is a quadruped is not a land-based creature. Because we know something about all quadrupeds (Let's assume this statement is true), we can say something about any other thing that belongs to this group. These a mathematician may call sets of things. When sets overlap, we can make statements about that overlapping, like the statement “All Tigers are land-based creatures.” What Aristotle sought in part was the connection that demonstrated how beings-at-work were motions in common, and these motions in common were causes in the sense that all causes had a kind of motion to them, which in turn was in part the formal and final cause and so the material eidos as well. Aristotle needed some kind of premise with which to make his arguments and he thus needed to observe first; he reasoned later with the observations made. The significance of Aristotle's contribution is that his metaphysics compelled him to create a method of observation and reasoning. He observed and sought what is the motion of a given thing and then reasoned in order to understand it more. The observation was for Aristotle a direct link to the nature of a given thing. Given the titanic influence Plato had on the ancient world, such an observational method concentrating on things that become rather than the being of things was a radical step towards what we now call science.
There were four kinds of statements that said something about the eidos, or the sets of different things. These are called categorical propositions. Notice the word “categorical.” One seeks categories of different things in the world and statements about them that are true. When these statements are made, they form sets of things that may be related to one another. The relation to one another reveals something new, another inference, about the subjects in the statements. One kind of statement made a claim about all of the members of a specific set of things. These are A statements:
All X are Y.
Every X is in the category of Y. The statement “All tigers are land-based animals” is just one such statement. All of the set of tigers are creatures in the set of land-based animals. Another statement made a claim about the exclusivity of the two sets. These are E statements:
No X are Y.
This statement means that of the set of Ys there are no Xs in the set of Y. This statement also means that none of the set of Y are in X because if there is no connection between Xs and Ys, then there must be no connection between Ys and Xs. These sets, or categories, are exclusive. “No tigers are sea-dwelling creatures” is one such statement. A third kind of statement means that some of one set of things is in another. These are I statements:
Some X are Y.
This statement means that there is at least one X, and it is in the same set of things as Y. There may be more than one X in the set of Y, but we are justified in saying that there is at least one. “Some tigers are animals friendly to humans” is one such statement. The fourth kind of statement is a negation of the third kind. These are O statements:
Some X are not Y.
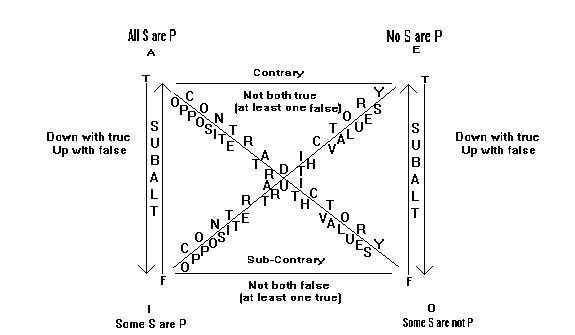
These assertions mean that there is at least one X, and that X is not in the set of Y. “Some tigers are not animals friendly to humans” is one such statement. One can see how observation of the natural world is imperative to making claims about certain things. When a statement is made, it means that there has been no reflection upon this natural occurrence other than to observe how one natural thing relates to another. The fixed relationships between the statements can be summed up by the traditional square of opposition, which shows the truth values of the four statements with respect to one another:
Universal statements are on the top and particulars on bottom. Universals are the whole of a set of things. The particulars are simply one or more of a set of things but not the whole set of things; they are, however, not necessarily specific manifestations of things, or examples. Affirmatives are on the left and negatives are on the right. The statements that run diagonal to one another are contradictories, which means they always have opposite truth values. “Some tigers are gentle friends” is contradictory to “No tigers are gentle friends.” It cannot be that the set of tigers has within it no gentle friends and some gentle friends at the same time. Given that any observational proposition is true, this relationship is a constant one. In other words, there is a certainty about the relationship between the statements given the existence of no gentle tigers as opposed to some gentle friends that are tigers. That certainty reveals something about the eidos of tiger and the eidos of gentle friends. The same kind of certainty is true for the relationships between other statements. Contraries are only on the top of the square; they cannot both be true at the same time. The statement “All tigers are quadrupeds” and the statement “No tigers are quadrupeds” obviously cannot be true at the same time. In fact, if one is true, then the other must be false. Contraries can, however, both be false at once. The statement “All tigers are fierce and dangerous” and the statement “No tigers are fierce and dangerous” are both false, if it is true that some tigers are fierce and dangerous. Notice that either statement can be true, given certain circumstances, but those statements together cannot both be true. Again, there are sets and sub-sets of things in the world that in some way coincide with one another and thus have the same or interlocking relationship, a simple example being that all tigers being fierce also means that some tigers are fierce. One end of being a tiger is fierceness and without fierceness in the tiger, a tiger would not have the arrangement necessary to be a tiger. Strikingly, sub-contraries are the opposite of contraries. Always one of the statements is true. If you know that one is false, then the other must be true. Yet, they may both be true. The statement “some tigers are fierce and dangerous” and the statement “some tigers are not fierce and dangerous” can both be true, but they cannot both be false. There must exist or not exist this particular combination of characteristics in tigers. In sub-alternation the truth falls down, so if an A statement is true, an I statement is true. If all Tigers are Cats, then surely some Tigers are Cats. Additionally, if I is false, then A is false as well. If it is false that some Cats are Turtles, then it must be false that all Cats are Turtles. Yet, vice versa is not the case. If I is true, then A may be true. If some Apes are orange Creatures, then perhaps all Apes are orange Creatures, but we cannot make that determination based on the knowledge that some Apes are orange Creatures. Alternately, if it is false that all Cats are Tigers, then it is not necessarily false that some Cats are Tigers. True universal categorical propositions and false particular categorical propositions are the most potent statements. If one knows that a universal proposition is true or a particular proposition false, one is able to derive the truth of all the other statements. Yet, false universal statements and true particular statements only grant the truth value of the contradictory. The expectation when comparing these statements seems to be to find universal statements about the interlockings of what things are, or more precisely how they move together. When we find the interlocking aspect of the comparison, we have identified a cause, like a formal and final cause of tigerness is ferocity. It is only one cause of tigerness, but we know something about them by means of observation and argumentation. In this sense, Aristotle's method is observational, but it is not properly a scientific method. Again, he creates no hypothesis that he then proves true by empirical observation. Aristotle existed at a time when most thinkers presupposed the world to be static, or constant in some sense. Change existed, but change was alteration and re-alteration rather than development or permanent alteration or dissolution. So, all things with natures have an unchanging eidos that moves themselves to it. Alteration seems to have involved the growth and decay from and into their own eidos in particular manifestations. Aristotle would not have believed that animals and plants and living organisms of all kinds evolve in order to survive. Perhaps this perspective limited the followers of Aristotle, yet his method was potent indeed. These statements cover a great deal of the observed natural world if used properly, and Aristotle understood their constant [xvii] relationships to one another, as there are supposedly regular and reliable relationships of the things about which they speak a truth.
What results are some informative relationships between things in the world revealed through observations and articulated in language. In other words, there are aspects of these statements that are themselves kinds of constant relationships that can be relied upon and so are constant relationships between things.
Statements and thus propositions must have specific elements to them in order to draw good inferences. The first element we will discuss is that of distribution. Distribution is of vital importance if one is to make that essential connection between sets of things. When one argues with syllogisms, one must know something about an entire set, or category, of at least one class of things. A set of things is distributed when a statement makes a claim about all of its members. Such certain knowledge of an entire set is necessary because an argument needs to have a foundation on which to stand. There must exist some kind of fundament in order for new information to emerge, and such certainty is that of the knowledge about some aspect of an entire set of things.
- All fierce animals are dangerous creatures.
- All tigers are fierce animals.
- So, all tigers are dangerous creatures.
One is able to say something about all tigers because they all belong to the set of fierce animals and the set of fierce animals, all of them, belong to the set of dangerous creatures (given the truth of the statements). One would not be certain that there exists some characteristic of tiger called “dangerous” unless there existed some certainty that all of them are fierce. Fierceness is a formal cause and a final cause to tiger only because there is a discussion about every tiger. If one were able to talk about only some tigers, then no necessary connection would be possible, only possible connections with an unknown amount of probability.
The relationships between specific statements always have particular facets. Given that the statements are true, one can establish certain relationships between things. There is a kind of clarity and certainty established by the working out of the specific relationships between categorical propositions, but it is important to recall that it is language-based. That is, the logic that emerges from the relationships between statements is mathematical in nature in the sense that there is knowledge of an entire set of things, but language expresses the observations rather than a mathematical formula. The reduced outline of something and the precision of mathematics is not Aristotle's aim. In fact, just as he complained about the Pythagoreans he would critique modern scientific method should he be alive today. Mathematics does not reveal that fullness of being-at-work in the universe of things. Later, mathematical reasoning will take a primary place, but for Aristotle's method logic and the observing of the overlapping of sets of things is language-based. Put simply, when one compares statements, one can see that Aristotelian propositions demonstrate certainties. There are three kinds of relationships worthy of note: conversion, obversion and contraposition. Each alteration of statements reveals specific relationships. Each relationship is one form of a constant, which is an important element in scientific (especially mathematical) reasoning.
Conversion means to switch the subject term with the predicate term. The conversion of an E statement or an I statement gives a new statement that is logically equivalent to the given statement.
E = “No tigers are fierce animals” becomes “No fierce animals are tigers.”
I = “Some tigers are fierce animals” becomes “Some fierce animals are tigers.”
The above statements mean essentially the same thing. Yet, converting an A or O statement does not necessarily make a logically equivalent statement. These converted statements may not have the same truth value as the given statement. So, given the truth or falsity of the first statement one cannot always determine the truth or falsity of the second statement.
A = “All tigers are fierce animals” is not the same truth value as “All fierce animals are tigers.”
O = “Some tigers are not fierce animals” is not the same truth value as “Some fierce animals are not tigers.
Note that only the subject and predicate have been exchanged. Otherwise, the statement is the same, yet the relationship between the existing things is not the same at all. Always these statements will have specific and reliable relationships to one another, given the truth of the observations. This reliability is one of the foundations of the logic that will in turn lead to inferences, which tell us something about the world that we did not know. Mathematics uses a form of these kinds of constants when it employs specific measurements like sine, cosine, tangent, π, πr² and the like. The truth value of a conversion or an A or O statement depends upon the content of the statement:
“All bachelors are unmarried men” becomes the equivalent “All unmarried men are bachelors”.
“Some apples are not oranges” becomes the equivalent “Some oranges are not apples.” Because of these given relationships, logically speaking, the converse of an A or O has undetermined truth value. Conversion may be used to provide the certain relationship between the premise and the conclusion of an argument:
- No Tigers are Beetles
- Therefore, no Beetles are Tigers.
-
- Some Dogs are dangerous Creatures.
- Therefore, some dangerous creatures are Dogs.
Always will one be able to conclude the above, given the truth of the statements. That is one certainty of the Aristotelian system, though it is not true that Aristotle achieves absolute certainty or truth. The premise of each argument form necessarily has the same truth value as the conclusion. So, if the premise is true, the conclusion is necessarily true. On the other hand, one is able to prove that an argument is invalid:
- All S are P.
- Therefore, all P are S. UNDETERMINED
-
- Some S are not P.
- Therefore, some P are not S. UNDETERMINED
If one says “All Cats are cuddly Creatures”, one cannot definitively make the statement “All cuddly creatures are Cats.” All of the set of Cats is in the set of cuddly Creatures, but that statement by itself does not say anything more than that. So, one cannot say something about all cuddly Creatures. The same is true for the O statements. Simply because some Dogs are not Creatures fond of cats says nothing necessarily about Creatures fond of cats. It only says that some Dogs are not in the set of Creatures fond of cats. Such a statement does not even mean that some Creatures fond of cats are not Dogs.
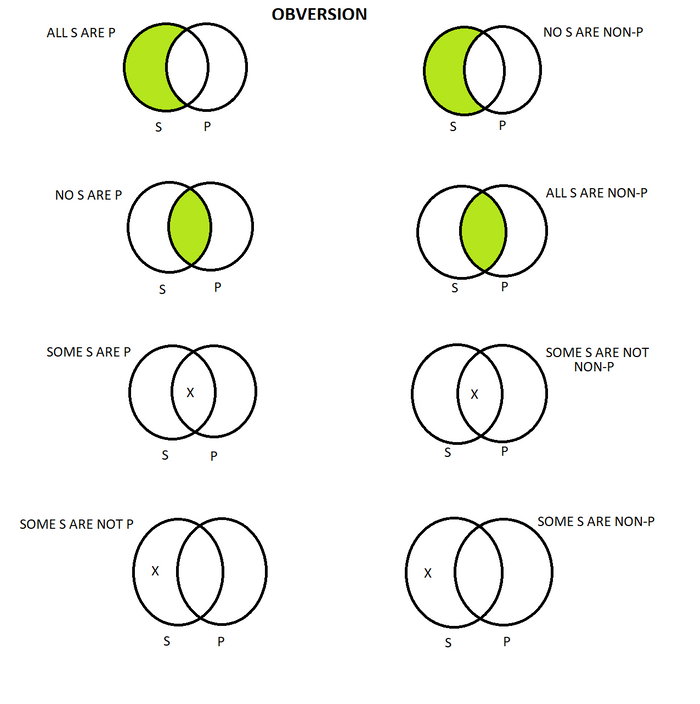
Obversion is another transformation of categorical propositions that Aristotle noticed have specific relationships. One changes the quality of the statements without changing the quantity, and one then changes the predicate with its term complement. The complement of a set is everything that exists outside the set. It is ordinarily expressed by using the prefix “non.” The term complement of “Tigers” is “non-Tigers.” The quality of a statement changes it from affirmative to negative or from negative to affirmative. So, “All Tigers are Animals” becomes “No Tigers are non-Animals.” One can see the relationships between the statements using a Venn diagram, which is a visual representation of the sets. Each circle represents a set of things. The “S” set is tigers and the “P” set is fierce animals. The colored areas are those areas where there is nothing in that section. The X represents at least one member of a given set; perhaps more but at least one.
One notices immediately that all the statements are logically equivalent, here represented by the shading of the same parts of the circles. One may suspect that obversion in itself says little or nothing about the expressed sets, but obversion provides one with immediate inferences that are as certain as other relationships between statements. Thus, the following statements are valid:
- All S are P.
- Therefore, no S are non-P.
- -
- No S are P.
- Therefore, all S are non-P.
- -
- Some S are P.
- Therefore, some S are not non-P.
- -
- Some S are not P.
- Therefore, some S are non-P.
These are simple, straightforward statements easily seen to be true, and that is their virtue. They provide the foundation for building a complex argument that reveals something about the world one did not before know: the inference. Again, Aristotle's system is language-based, rather than mathematics based, yet there exists in it an element of mathematical certainty because of the reliable relationship between the propositions.
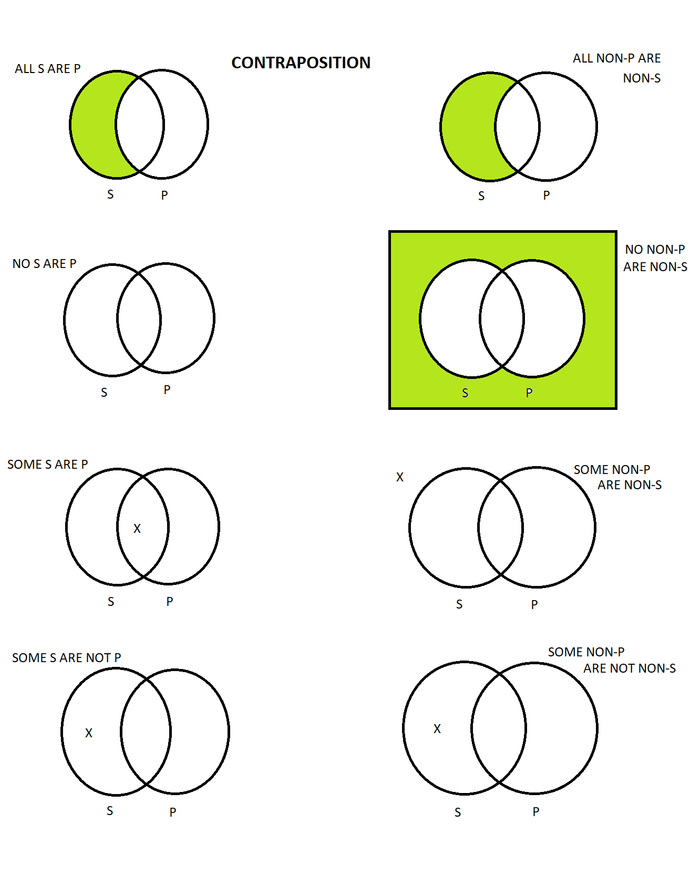
Contraposition is our final transformation of statements. In order to contrapose a statement, one switches the subject and predicate terms, then replaces both the subject and predicate terms with their term complements. The statement “All tigers are fierce animals” becomes “All non-fierce animals are non-tigers.” In half of these transformations the truth value is equivalent. In the other half, there come about significant changes. The Ss are the tigers and the Ps are the fierce animals.
- The following conclusions can be determined by the contraposition of A and O statements:
- All S are P.
- Therefore, all non-P are non-S.
- -
- Some S are not P.
- Therefore, some non-P are not non-S.
- Again, these statements are simple and they immediately reveal something about the universe, given that they are true. Contraposition also allows us to know when a statement is illicit. Each of the following are fallacies:
- Some S are P.
- Therefore, some non-P are non-S. FALLACY
- -
- No S are P.
- Therefore, no non-P are non-S. FALLACY
In the first example, one says something about some S, but nothing about non-P. One cannot say that because something is not P, it must be not S. The same is true for the second statement. The statements that remain transform into new assertions. “No S are P” contrapositions into “No non-P are non-S”, which means that all things outside the set of P are inside the set of S. The statement “Some S are P” contrapositions into “Some non-P are non-S”, which means that some things outside the set of P are also outside the set of S. All of these statements tell us something about the universe and assist in determining causes and thus reveal the being-at-work and what-it-is-to-be of different things. We will see that Euclid and Archimedes employ a similar kind of reasoning. They create systems of thought based on what they believe to be certainties. In the case of Aristotle, there are certainties of relationships between statements. In the case of the mathematicians there is certainty of mathematical propositions. But we need to cover the form of the syllogisms and some of the rules for logic that Aristotle articulated. These are intended to create guidelines for the most certain relationships that lead to clear and true inferences.
First, there is such a thing called a syllogism. A syllogism is a set of statements like we have seen repeatedly. The first two assert something about the universe and the third uses the commonality between the two to assert something new about the universe. Here is one of our examples:
- All fierce animals are dangerous creatures.
- All tigers are fierce animals.
- So, all tigers are dangerous creatures.
- We have two sentences that articulate observations about certain characteristics of animals, specifically tigers. The third, as we have seen again and again, makes use of their relationship to one another. One proceeds from an observation one believes to be true to new information. Such an argument is a categorical syllogism. A categorical syllogism is an argument that contains categorical propositions, each of which is one of the four types of propositions we have already seen:
- A: All x are y.
- E: No x are y.
- I: Some x are y.
- O: Some x are not y.
The standard categorical syllogism consists of two premises and a conclusion, each of which is one of the above forms. We have already seen many of them, but here is an example:
- Ex. 1:
- All humans are living beings.
- All science students are humans.
- Therefore, all science students are living beings.
Note that the statements in this example happen to all be of type A. There is no necessity that a syllogism have all statements of the same type; any combination is possible. There are specific parts of a syllogism that need to be in specific places, and one must know the parts of a syllogism in order to form one properly. An improper syllogism will not provide the certainty of the relationships between the statements.
The Middle Term—The middle term is a word or a phrase that occurs in both premises. (The letter “M” represents it in the diagrams below).
The Minor Term---The minor term is the subject of the conclusion.
In a standard-form syllogism, the premise that contains the minor term (called the minor premise) is part of the second premise (as in Ex.1). In order to determine if a syllogism is in standard-form, one starts with the conclusion, checking to see if the premise containing the subject of the conclusion is in the second premise. If it is, the syllogism is in standard-form; if it is not, one must place the syllogism in standard-form by reversing the order of the premises (“S” represents the minor term in the diagrams below). The minor term must always be the subject of the conclusion in order to set the syllogism in standard form, but the minor term may appear as either subject or predicate in the minor premise.
The Major Term—The major term is the predicate of the conclusion. In a standard-form syllogism, the premise that contains the major term (called the major premise) is part of the first premise (see Ex. one). If the premise containing the predicate of the conclusion is part of the first premise, the syllogism is in standard-form; if it is not, one must configure the syllogism in standard-form by reversing the order of the premises (“P” represents the major term in the diagrams below). Although the major term is always the predicate of the conclusion, this term can appear as either subject or predicate in the major premise.
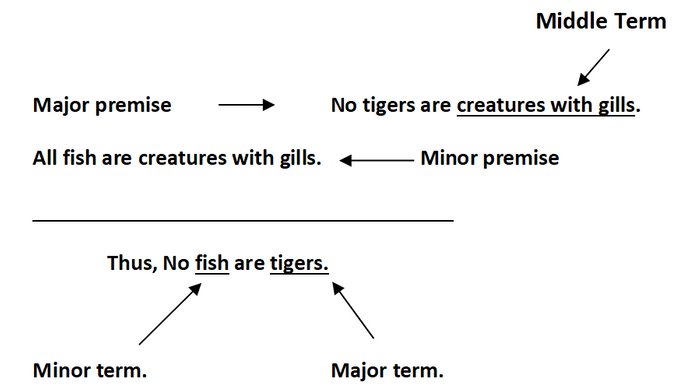
Ex. 2:
The Parts of a Syllogism Placed in Standard-Form
The above argument has the following structure or argument-form:
- No P are M
- All S are M
- No S are P
P is the major term (in this case “tigers”), M is the middle term (in this case “creatures with gills”, and S is the minor term (in this case “fish”). The logical validity of a syllogism [xviii] does not depend on its content but only on its logical form, and the form of the argument is what gives it certainty. That is, there are specific relationships between these statements and a specific interlocking, or non-interlocking, that bring out clear and certain conclusions. This logical form is the certainty that Aristotle found in the relationships between these specific statements, similar to the relationships between the converted, obverted and contrapositioned above; these statements have certain relationships and that certainty is needed in order to form valid and sound arguments. One can see how standard form is important, if specific statements have specific relationships to one another. The form must be of a certain kind in order to make the connection. Logical form is akin to mathematical precision, and determination of the logical form of a categorical syllogism depends on two aspects of a syllogism, the mood of the syllogism and the figure of the syllogism. [xix]
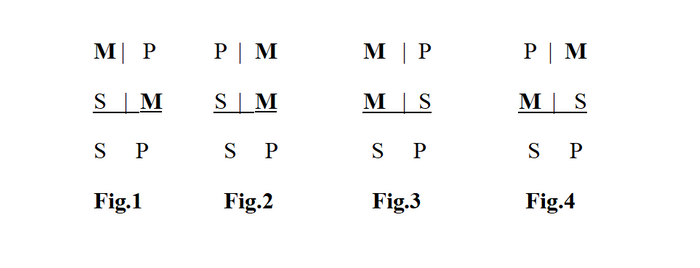
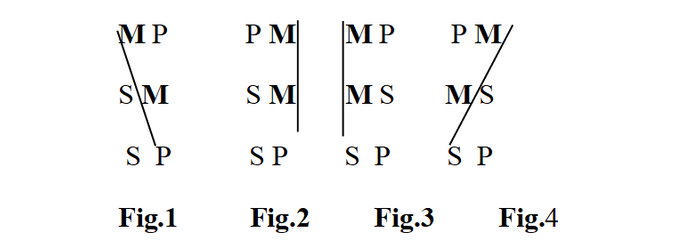
The Four Figures of a Syllogism help determine the validity of a syllogism. These are structural parts of the argument without which the certainty of the relationship between the statements cannot exist. The figure of a syllogism refers to the positioning of the middle term. As we have seen, the middle term is the term that appears in both premises. There are four kinds of figures (i.e. four possible configurations of the middle term in a syllogism):
Notice that there is a shirt collar pattern below made by the placement of the middle term when the four figures are presented in order, 1-4. This pattern helps to determine what figure is what. In other words, in Fig. 1, the middle term slants down and to the right, i.e. it is the subject of the major premise and the predicate of the minor premise. In Fig. 2, the middle term is the predicate of both premises; in Fig.3 the middle term is the subject of both premises; and finally, in Fig., 4 the middle term slants up and to the right, i.e. the middle term is the predicate of the major premise and the subject of the minor premise.
The mood of a syllogism is the list of the types of categorical propositions that appear in a syllogism. Remember that the four types of categorical propositions are the following:
A All X are Y.
E No X are Y.
I Some X are Y.
O Some X are not Y.
The mood of example one is AAA (i.e. it has all A-type of statements as its component statements).
- Ex. 1:
All humans are living beings.
- All science students are humans.
- Therefore, all science students are living beings.
One can determine the mood and figure of any syllogism with relative ease. Here are some other examples:
- Ex. 2:
No spoons are wombats.
- All wombats are jesters.
- Thus, No jesters are spoons.
- EAE-4
- -
- Ex.3:
Some cosmonauts are grass-eaters.
- No mammals are grass-eaters.
- Thus, Some mammals are not cosmonauts.
- IEO-2
- -
- Ex.4:
No gorillas are dogs.
- All gorillas are light bulbs.
- Thus, no light bulbs are dogs.
- EAE-3
One indicates the figure of a syllogism by placing its number right after the three letters that represent that syllogism’s mood. Again, syllogisms must be in standard form in order for the determination of validity to take place. One cannot make a good determination of the relationship between the statement-types unless the statements are arranged properly. The premise that contains the minor term is called the minor premise and the premise that contains the major term is called the major premise.
Distribution of Terms As we have seen, a term is said to be distributed in a given proposition if that proposition makes an assertion about all of the members of the set denoted by the term. In the statement “All cats are animals”, the term “cats” is distributed, because we are saying something about all cats; but the term “animals” is not distributed because we are not saying something about all the animals. In “No dogs are cats” both terms are distributed; we are saying of all dogs that they are not cats, and also we are saying of all cats that they are not dogs. In the statement “Some cats are healthy animals” neither term is distributed. We are not saying anything about all cats, but only about some of them; likewise we are not saying anything about all healthy animals, but only about some of them. In the statement “Some cats are not healthy animals” only the predicate term, “healthy animals” is distributed; we are saying something about all healthy animals here; we are saying of all healthy animals that there are some cats that are not any of them. We want to find the connection between the statements and that connection refers to all of a specific set of things. Distribution makes this connection possible. One distinguishes valid from invalid arguments in part by knowing the distribution of terms:
A All S are P. ONLY THE FIRST TERM IS DISTRIBUTED
E No S are P. BOTH TERMS ARE DISTRIBUTED
I Some S are P. NEITHER TERM IS DISTRIBUTED
O Some S are not P. ONLY THE SECOND TERM IS DISTRIBUTED
Once we have understood these aspects of categorical syllogisms, we are able to use observations to form arguments and thus make inferences about the things in the world. There are five rules for determining the validity or invalidity of syllogisms according to Aristotle. [xix]
Rule one: No valid syllogism has two negative premises. Any syllogism possessing two negatives premises is necessarily invalid because there is no connection between the sets of things. Thus, the following syllogisms possessing the following moods are invalid: EEE, EEA, etc., EOA, EOE, etc. OOA, OOI, etc. One cannot draw an inference from these specific combinations of statements.
Rule two: If a valid syllogism has a negative premise, it must have a negative conclusion; if it has a negative conclusion, it must have a negative premise. All syllogisms violating this rule are invalid, so one can see immediately that syllogisms with the following moods are invalid: EAA, OII, AIE, IAO, etc. Here a similar relationship holds true. If there is a negative relationship, then the syllogism is saying that there is no connection, so it must conclude that there is another lack of connection between sets of things.
Rule three: The middle term of a valid syllogism must be distributed at least once in one of the premises. A syllogism with a mood of IIA, IIE, etc., will be invalid, because the middle term cannot be distributed in a syllogism that has two “I”-statements as premises. “I” statement-types distribute none of their terms, and so there is no interlocking or connection between the sets of things it discusses. The figure and mood strictly determine if the middle term is distributed. Their strictness is mathematical in that, again, a firm connection must emerge between sets of things. If the middle term does not describe an entire set of things, then one cannot say something about all of them. A numeric quality to the word makes language potent in an argument. The following syllogism-form is AAA-2:
- All P are M
- All S are M
- Thus, All S are P.
The middle term is distributed in neither premise, because the first term alone in an “A” statement is distributed. So, the middle term is not distributed. This syllogism-form commits the Fallacy of Undistributed Middle, and so is invalid. Here is an example:
- All dogs are animals
- All cats are animals.
- Thus, all cats are dogs.
This statement says nothing about the set of all animals, and so there is no necessary reason that because cats and dogs are animals they are the same animals. The necessary reason would be present should the term that makes their connection certain be distributed. The middle term must be distributed only one time for the necessary connection to be present. Thus, AAA-1 is a valid syllogism form; an AAA-1 syllogism distributes its middle term in the major premise:
- All humans are animals.
- All men are humans.
- Thus, all men are animals.
This syllogism is valid because it makes a statement about an entire set of things, humans, that bridges the gap between the other statements. All men are humans, but all humans are animals so all men is a subset of all humans and all humans is a subset of all animals. All men must be a subset of all animals. Here is the certainty, and that certainty is reached only when the syllogism has a specific form to it. One bases a conclusion on the observation inherent in the first premise.
Rule four: Any term distributed in the conclusion must be distributed in a premise. This rule concerns the major and minor terms. If they are distributed in the conclusion, they must be distributed in the premises as well. The same reason applies. If one says something about the whole set of things in the conclusion but they did not make an assertion about the whole set of things in a premise, then there is an unjustified leap of reasoning because the whole set of things is the connection between terms. One cannot say that some tigers are fierce and then suddenly say all tigers are fierce. Thus, a syllogism with an “E” statement conclusion will only be valid if both the major and minor terms are distributed in the premises as well. Should the conclusion of a syllogism be an I-statement, clearly one would not need to concern oneself about this rule, since neither term is distributed in its conclusion. Should the conclusion of a syllogism be an A-statement, and thus the minor term is distributed in the conclusion, one would be compelled to determine if it is distributed in the minor premise as well; should the conclusion be an O-statement, and thus the major term is distributed in the conclusion, one would be compelled to determine if that term is distributed there as well. Should a syllogism have a term that is distributed in the conclusion but not in the premise in which it appears, that syllogism would be necessarily invalid. Two fallacies may arise from violating this rule: Fallacy of Illicit Major and Fallacy of Illicit Minor.
Any EAE-4 syllogism we know has the following structure:
- No P are M
- All M are S.
- No S are P.
Both terms are distributed in the conclusion, so the conclusion says something about all of the set of S and P. A valid syllogism of this kind, according to rule four, must possess distributed S and distributed P in order for the connection to be necessary and strong. S is not distributed and P is distributed, so EAE-4 commits the Fallacy of Illicit Minor. It is invalid. If we look at a syllogism of the form AEE-1, we see that a slightly different problem arises.
- All M are P
- No S are M
- No S are P
Both terms are distributed in the conclusion, but the major term P is not distributed in the major premise because we are not talking about the whole of its set. So AEE-1 commits the Fallacy of Illicit Major. It also is invalid. Again, in order for Aristotle's kind of logic to be correct, it must say something about whole sets of things. If no whole set of things is assumed, then the argument makes no necessary conclusion and one cannot draw proper inferences. Thus, the certainty of the needed connection takes on a mathematical quality not only because it makes an assertion about an entire set of things, but also because the validity of the argument relies on the necessary connection resulting from statements that are certain. The statements must be categorical indeed in order for basic Aristotelian logic to operate correctly.
Rule five: One cannot draw a particular conclusion from two universal premises without making further assumptions in addition to the two premises. This much more modern [xx] rule relies upon the assertion that universal statements are interpreted to make no claims one way or the other about the actual existence of the things referred to by their terms. If one asserts that “All sphinxes are unnatural creatures”, according to this interpretation of the meaning of universal claims, one really only says “If anything is a sphinx, it is an unnatural creature”, and one is not actually asserting that sphinxes exist. But if one makes a particular affirmative or particular negative (an “I” or an “O”) assertion, one is claiming that something exists; “Some S are P” implies that at least one S and P exists, and “Some S are not P” implies that at least one S exists. Rule five thus asserts that one cannot draw a necessary inference from premises that make no assumptions about existing things. In other words, if one says something about things that do not necessarily exist, then one cannot say in the conclusion that they exist. This rule asserts that syllogisms with the moods AAI, AEO, EAO, etc., cannot be unconditionally valid. Such syllogisms have conclusions that imply the existence of some members of the sets denoted by their terms, but premises that by themselves do not authorize such assertions. These syllogisms commit the Existential Fallacy. Still, if a syllogism does not violate the other four rules but only violates rule five, it can be considered conditionally valid–valid if one assumes that the relevant sets denoted by the specific terms actually exist. For example:
- All big cats are living beings
- All leopards are big cats
- Thus, some leopards are living beings.
This syllogism is AAI-1. It commits only the existential fallacy and so it is conditionally valid, valid on the condition (in this case) that leopards and big cats really exist. If the last premise had been “All leopards are living beings” the argument would have been unconditionally valid because, as interpreted here, universal statements do not make claims about existence; “All big cats are living beings” only means “if there are any big cats, they are living beings.” In that case the rule five would not be violated. If one chooses to interpret universal statements as making claims about existing things, we would be following Aristotle more closely, who in his discussion of the square of opposition asserted that one can validly infer “Some x are y” from “All x are y”. But Aristotle assumes that the ‘x’’s and ‘y’s in question exist. Rule five asserts that if one proceeds from universal claims [like A- or E-type statements] to a particular conclusion [an I- or an O-type statement] then one attempts to infer the existence of at least one thing from premises that do not assert the existence of anything. Yet, in Aristotle’s square of opposition the A- and E- type statements do assert the existence of things. We will follow the ancient tradition because we are talking about ancient science, but it is appropriate to know the modern rule in order to understand how in some instances the ancient kind of thinking differs from the modern.
Here are the five rules for valid syllogisms, including the existential fallacy:
Rule 1: No valid syllogism has two negative premises.
Rule 2: If a valid syllogism has a negative premise, it must have a negative conclusion; if it has a negative conclusion, it must have a negative premise.
Rule 3: The middle term of a valid syllogism must be distributed at least once.
Rule 4: Any term that is distributed in the conclusion must be distributed in a premise.
Rule 5: You cannot draw a particular conclusion from two universal premises (without making further assumptions in addition to the two premises).
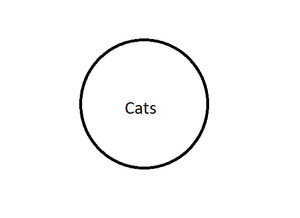
Again, if a syllogism does not violate a single rule, it is unconditionally valid. If a syllogism does violate a single one of the first four rules, it is invalid. If a syllogism conforms to rules 1-4 and only violates rule 5, then it is conditionally valid. Such a syllogism could be valid if certain assumptions are made regarding the existence of the sets discussed. One may see easily how Aristotle's rules and his system work by looking at Venn diagrams, which are visual representations of arguments (already seen above). Venn diagrams were invented by John Venn more than one-hundred years ago, but they are so effective that they remain in use today. Each circle represents a set of things in the universe.
This circle represents all the cats that exist in the universe, but the set of cats is quite large.
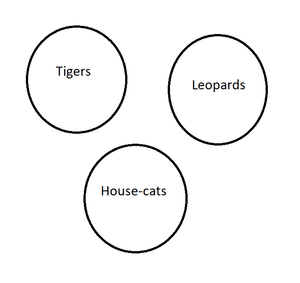
So, one needs to separate the sets in order to see what set belongs to what category. Each circle, or set, represents something about the set of cats.
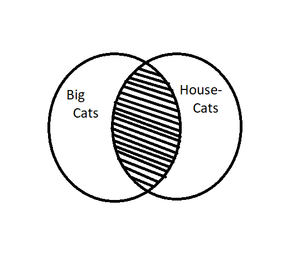
The set of tigers, for example, belongs completely inside the set of cats, as does the set of house-cats. Yet, clearly there are differences between them. So, one needs to determine where they overlap in order to demonstrate the difference. When there is nothing in a set of things represented by the circles, that area is shaded. This set of circles indicates that no house-cats are big cats.
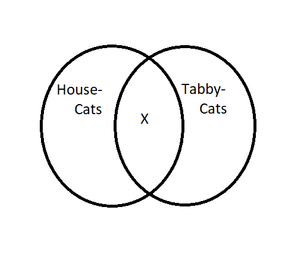
One can use the circles to represent any set of things. When there are some or at least one in a set of things, an “X” represents that particular in a set. In this set of circles, some house-cats are tabby-cats.
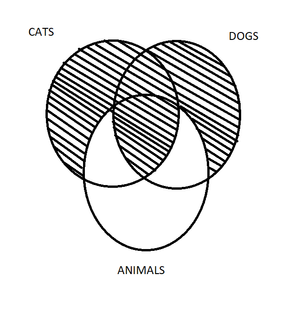
One may then use three circles to represent the three sets of things in any argument. So, these circles indicate “Cats”, “Dogs” and “Animals.” All of the set of cats and dogs are in the set of animals and none of the set of cats are in the set of dogs nor is the set of dogs in the set of cats, but not all animals are in the set of cats or the set of dogs.
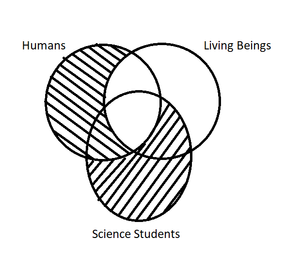
Notice that each of the circles represents a number of things that may exist in the universe. One can represent simple arguments with these circles, and how things relate to one another becomes clearer. This diagram illustrates the following argument:
- All humans are living beings.
- All science students are humans.
- Thus, all science students are living beings.
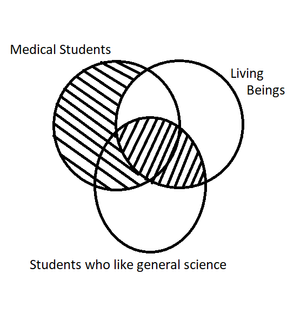
This diagram illustrates the following argument:
- No living beings are students who like general science.
- All medical students are living beings.
- Thus, no medical students are students who like general science.
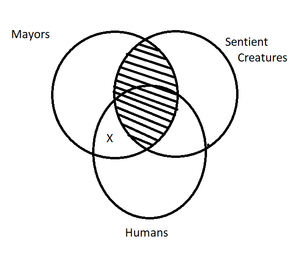
When only some of a particular set find themselves in another particular set, the overlapping has an X in the space where the two sets overlap. This diagram illustrates the following argument:
- No mayors are sentient creatures.
- Some humans are mayors.
- Thus, some humans are not sentient creatures.
For our purposes the circles represent not only sets of things and therefore they have a mathematical element to them, but they also represent the eidos of Aristotle, so to speak. In other words, they are different sets of things that share a kind. There is some aspect of a cat, for example, that transcends the set of house-cats. It is some arrangement of the creature: four legs, fur, a specifically shaped head, a tail. Cats have specific ends, which is to say that cats become, well, cats. They move toward the end of being cat. As many sets of things as one wishes to examine are as many sets that may be formed into an argument. But each argument represents a number of sets of things. Aristotle's rules of logic demonstrate how sets of things interlock and interact with one another. Additionally, Aristotelian argumentation is a classification of things based upon observations. When the sets of things have specific relationships, like we saw when we compared how each statement-type relates to other statement-types, one can draw an inference about them. One knows more about the universe. Thus, Aristotle had an inductive aspect to his methods. He observed and used observations in order to make inferences about things that have a nature. Then, he argued about their function. What he discussed was biological formation of animal parts, or even the reproductive organs of animals. Again, he was the first biologist.
So, Aristotle explained the physical processes of animals and things in part through causes. These causes were the material, motive, formal and final causes. Each one of these causes can be interpreted as influenced by the Platonic eidos. The Platonic eidos was a deeper aspect of reality, one which had no spatial or temporal “being” to it. Aristotle makes his formal cause the arrangement or organization of what something is. An organization of something is what a thing with a nature moves into, which is itself. Movement is thus an aspect of something's being, a kind of being-at-work accomplishing the task of becoming itself. Its work-being may be called energeia, which the term from which we derive the word energy. It literally means “the work within” or “in the work.” This activity is a kind of actuality that in turn is a potential to be something else. Thus, bronze is an activity that makes bronze into itself, and bronze is the potential to be a sword, or a statue, even a candle holder. So, the formal cause moves into itself in order to attain its end, which is the final cause. The final cause is the goal or end of something, which again is itself. The goal of the bronze is becoming bronze, or the activity that leads to the becoming that comes to be and continues to be bronze. In this way the formal cause and the final cause are the same, since the arrangement that makes something itself is its own end, at least for Aristotle. The motive cause is the most scientific cause that Aristotle articulates. It is the activity of one thing that begins the activity that is another thing. A man reproduces and creates another human through this cause. The act of one boulder striking another is a motive cause of an avalanche. These are the activities that come from each thing doing what it is that it is, like a tumbling boulder.
Aristotle had almost no interest in this cause, and it is this cause that most closely resembles the sense of scientific cause so prevalent today. In fact, the formal cause, the final cause and even the material cause are virtually non-existent in the discussions engaged in by the scientific community. The material cause may be interpreted in several ways, but it is essentially necessary that if something has an activity that makes it what it is, and if what it is ultimately has a formal and final cause to it, then even material has a formal and final cause to its becoming. In that sense, material itself is form, and because the eidos of Aristotle is a part of form and arrangement, all of Aristotle's causes have an aspect of eidos to them. The eidos is investigated by the observations that lead to inferences, which in turn present new and deeper insights about things in the world. So, the investigation into how sets of things overlap and interlock is the investigation of the eidos of things and thus their causes. Aristotle has developed a method that brings out the activity of something that explains not only how it influences objects around it, but also what it is and what purpose it has. It is in this sense that Aristotle's thought is scientific; it is analytic. His inductive method means that we are able to say something about how the different sets of things are part of, potential for, subject to or even responsible for one another. The certainty of a properly ordered argument is the kind of certainty Plato sought in the immaterial world. It is the eidos of Plato put into matter, and that is what moderns call metaphysics and not science proper. The deductive aspect of Aristotle's thought is the clarity of being-at-work and what-it-is-to-be of a given thing. We have not only found what something is, but we have found what-it-is-to-be, or its potential by making use of certain statement relationships as well as specific forms of propositions (premises). The resulting insight grants human being enormous power over what it analyzes, and it gives much more precise analysis to those who seek to control and manipulate nature. Such is the potency of his analytic method. In other words, we can be certain of some partial relationships. We can be certain of other complete relationships. We can make universal statements about things in the world.
Science answers the question how something has come to be and Aristotle is scientific in the sense that he is analytic, but he also has included the standard sense of cause in his investigation. In this sense, Aristotle's analytic method is more broad and ambitious than science. Many hard scientists believe that philosophers want to obtain absolute answers, and some do. But the most worthwhile of thinkers are philosophical in the sense that they admit to ignorance. They do not claim to know. Aristotle's analytic system is on the whole desultory. It seems as if he sometimes does not conform to his own expectations because he was able to classify his topics in a more systematic way, but he does not appear to do so. Additionally, what remains of his corpus is a mess of writings that may not have been intended for anyone to read. So, we do not know the extent to which Aristotle's work was systematized. There is much that has been lost. There may well have been long works detailing the causes of different animals, political systems, being and other topics that have fallen into oblivion through neglect or deliberate destruction. Whole scores of Aristotelian followers may have amassed observations that transformed into notions of how things work. We do not know fully what the Aristotelian school produced. Yet, what we have tells us that his analytic system was capable of classifying practically any topic, which is precisely what science has done with virtually any human inquiry today. We will see other thinkers, a new kind of mathematician, make still stronger arguments, but they do not analyze nature. They analyze a framework that leads to hypothesis, which will eventually be empirically verified. Aristotle investigated in a more full sense what is there.
Notes
- [i] See Glanville Downey.
- [ii] It is important to note that Aristotle's surviving work is sometimes contradictory and corrupt, resembling the desultory state of a rat's nest. What scholars possess are parts of his esoteric works, or works that were not meant for what we now call publication. Some scholars believe these writings to be notes, perhaps for purposes of lecture or student notes. The state of his work makes interpretation quite difficult, and how one interprets Aristotle depends largely on what one thinks he must have meant. Our interpretation concentrates on his causes and the genesis of his logic rules. Like Plato, more thought is always necessary when interpreting Aristotle, no matter how much one has already contemplated his work.
- [iii] Aristotle thought that one could argue to first causes, which may mean that all of the above-listed parts are necessary in order to determine a first cause for a given science. That is why we talk about many aspects of his thought, in order to understand why there is one sense in which he has no first principles and in another sense he asserts many. Jaakko Hintikka puts it succintly, saying a particular science “is characterized by its subject matter, that is, by the genus of objects it is about.” Aristotle even states that “a single science is none whose domain is a single genus.” (Post. An. I, 28, 87a38). For more, see Wilson, Irwin, Hintikka.
- [iv] De Santillana and Reiche describe how the Platonic eidos is shifted from its metaphysical place in Plato to an actualization that manifests potential in Aristotle. Rihill believes, perhaps rightly, that ancient thinkers “did not so much stand on their predecessor's shoulders as knock them down, step over them, and go elsewhere.” Perhaps it was not quite so eristic. Loux and Lewis articulate some interpretations as to how form and matter combine in particulars. Marjorie Grene points out correctly that Aristotle's use of eidos and genos is chaotic.
- [v] The phrase being-at-work is taken from the Joe Sachs translation of Aristotle's Physics.
- [vi] He did, however, accept Empedocles' four “roots” as elements of the moving universe, and Aristotle did believe that one can argue toward first principles (See Irwin). Matter seems to have as part of its structure a play of opposites, which is one way of interpreting earth, air, fire and water. Matter may also be thought of as a substratum, which may also be called prime matter (Patrick Suppes), but the nature of something, as a material eidos, is more its “what” than the matter comprising it. For a good review of the Aristotelian causes, see Falcon.
- [vii] One must be careful here to note that interpreting prime matter as an indeterminate mass of potentiality is the traditional view. A new view that demands prime matter to be of some kind of characteristic is emerging. For the traditional view, see Luyten, H.M. Robinson, For the emerging and other views, see Barrington Jones, Margaret Scharle, Sarah Broadie (who claims that substantial change does not require prime matter). M MacKinnon suggests how this belief came to be. Traditionalists try to demonstrate how prime matter is a something, like spatial extension; it is able to move and cease motion. See also Charlton and Fine. One must acknowledge Aristotle himself: “Matter qua matter is purely potential and without attributes.” (Metaphysics, 1029a19) and “the matter of the heavy and light, qua their matter, would be the void.” (Physics, 217b22).
- [viii] Mohan Matthen and R.J. Hankinson describe what amounts to the fullness in Aristotle when they talk about Aristotle's non-reductionist philosophy; the “parts are ontologically and causally subordinate to wholes.” His way of analyzing things recognizes not only the constitution of the whole by the part, but material causation is subordinate to formal causation. Such subordination is another way of making the eidos primary. E. Drabkin touches on the same issue when he states that conceptually force remains a qualitative conception, though Carteron correctly points out that forces cannot be entirely subordinated because they represent an early attempt at quantitative formulation. So, principles like inertia do not receive the bare-bones treatment needed for a proper theory of dynamics in Aristotle. Aristotle thus theorizes that a force constantly applied to an object will merely continue that objects motion rather than continually accelerate it (see Drabkin and Carteron). For these scholars Aristotle did not sufficiently abstract from the particular cases sufficiently to think in terms of the primary actors without all of the accidents, like elements that interfere with motion. One must always acknowledge Aristotle: “...a body must either remain at rest or be moved ad infinitum unless something stronger obstructs it.” (Physics IV, 8, 215a 19-22). He rejected the idea.
- [ix] Richard Pettigrew talks of a special way that geometry belongs to the sensible realm. His interpretation differs from a more traditional view, like that of Edward Hussey and Ian Mueller. Because Aristotle writes in a dialectical manner, there is much debate about quantitative and qualitative reasoning and many other issues. Joe Jones explains what may be thought of as intelligble matter as it relates to magnitude and thus mathematics. The issues of math, matter and magnitude are by no means clear-cut in Aristotle. For a better understanding of the differences between Aristotle's syllogisms and mathematical reasoning, see Kneale, Hintikka, Mueller, Wilson.
- [x] One can see, then, Aristotle's adaptation of the Platonic eidos as something moving from and into its own manifestation through and as matter. Its manifestation is itself a material eidos, but it is an eidos that moves into potential and actuality. Plato called this act of becoming not being, but participation. Participation is matter taking on an eidos as its fundamental reality, matter not really being anything other than that primordial formless and formable mass. In some ways the Platonic eidos is form, in some ways shape, in some ways motion, but it is not well articulated in any of these phrases. In sum, Aristotle brings the Platonic eidos into matter and becoming and so makes of it something empirically analyzable and graspable. In brief, the Aristotelian eidos is much more scientific.
- [xi] For an investigation into the phenomenological tone of Aristotle's observations, see Sean Kirkland, Dialectic and Proto-phenomenology in Aristotle's Topics and Physics.
- [xii] De Santillana and Reiche have an interesting take on the desire for the prime mover. It is the Good of Plato. The celestial sphere is perfect, as Lear vehemently asserts when he claims that mathematical properties are perfectly instantiated among the satellites.
- [xiii] Andrea Falcon points out the ambitious project of Aristotle, which attempts to establish the correct connections between things. These are rightly called explanatory connections and the whole of the universe is causally related as it is interconnected with form, matter and relationships. Nature is a topic of study materially, but not merely materially, if we are to trust Falcon. Patrick H. Byrne articulates the stages of Aristotle's scientific investigations.
- [xiv] This translation is A. J. Jenkinson's. Found here: http://libertyonline.hypermall.com/Aristotle/Logic/Prior-Analytics.html
- [xv] The phrase “what-it-is-to-be” is taken from Joe Sachs translation of Aristotle's Physics.
- [xvi] Aristotle explores formal and final causes of biology in his Parts of Animals. He explores material and motive, or efficient, causes in his Generation of Animals. He seems to have been the first biologist, but strangely he did not make use of his own logic rules and observations in order to create a systematic account of a given topic, as one would expect. Perhaps he left such work to his students or perhaps the systematic works that he wrote have all perished.
- [xvii] Aristotle not only established rules for logic but he also gave to Euclid many of the methods found in Euclid's Elements. The constants that appear in Aristotle's logic are mathematical in the sense that they are reliable relationships whereas mathematical constants are abstractions that are always true. There is debate on the differences between the two men's theories. Solmsen, Barnes and Ross argue over the origin of the theory of demonstration. H.D.P. Lee claims that Aristotle's definitions correspond to Euclid's definitions, Aristotle's axiomos to Euclid's common notion, and Aristotle's primitive existence claims (hypotheses) to Euclid's P1-P3. Yehuda Rav points out that modern mathematicians do not work with axioms even though they may be necessary and the division between axioms and definitions is not marked. There even exists a work that put Euclid's first six books into Aristotelian syllogisms: Analyseis Geometricae Sex Librorum Euclidis (Herlinus and Dasypodius). For a detailed explanation as to why the Aristotelian syllogism cannot be used strictly in a Euclidean proposition, see McKirahan. For more on this issue in general, see Taisbak, Maziarz and Greenwood, Russo, Bloom, Lear. It is best to remember that logic is not monolithic, but malleable and Aristotle's and Euclid's systems are one of many permutations of logic.
- [xviii] Remember the difference between logical validity and logical soundness. A syllogism can be logically valid even if it has false premises or a false conclusion; indeed, it can be logically valid even if it contains nonsensical statements, provided only that if the premises were true, the conclusion would have to be true. Recall too that all sound arguments are valid arguments having all true premises.
- [xix] Although Aristotle realized the importance of the concepts of figure, mood and distribution and understood most of these rules, the following formulations of them are taken from Patrick Hurley’s AConcise Introduction to Logic. Aristotle's articulation of logical relationships and logic rules is arranged quite differently and what we here review is a distilled version of his logic analysis. See Aristotle's Prior Analytics and Posterior Analytics for his much more nuanced understanding of logic.
- [xx] Aristotle is not responsible for rule five. Rule five came about as the result of modern logicians analyzing logical inferences. Aristotle would have believed that statements about entire classes of existing things are just that: statements the extend over an entire, existing class. Modern science is inductive. It does not make absolutely universal claims about nature and the laws of nature. Ancient thinkers, however, did.
- [xxi] See introduction to Generation of Animals. Aristotle, Generation of Animals, Harvard University Press, 1979. Trans. A.L. Peck. Loeb Classical Library.
ARISTOTLE BIBLIOGRAPHY:
- Balme, D.M. 1939. “Greek Science and Mechanism: I. Aristotle on Nature and Chance”, The Classical Quarterly 33, No. 3/ 4: 129-138.
- Barnes, Jonathan. 1984. Complete Works of Aristotle vols. I & II. Princeton: Princeton University Press.
- Barrington, Jones. 1974. “Aristotle's Introduction of Matter”, The Philosophical Review 83, No. 4: 474-500.
- Bärthlein, Karl. 1965. “ÜBER DAS VERHÄLTNIS DES ARISTOTELES ZUR DYNAMISLEHRE DER GRIECHISCHEN MATHEMATIKER”, Rheinisches Museum für Philologie, Neue Folge 108: 35-61.
- Beavers, Anthony F. 1988. “Motion, Mobility, and Method in Aristotle's "Physics": Comments on "Physics" 2.1.192b20- 24”, The Review of Metaphysics 42, No. 2: 357-374.
- Bicknell, P.J. 1961 “THE FOURTH PARADOX OF ZENO: An Interpretation of Aristotle Physics 239 B33 — 240 A18”, Acta Classica 4: 39-45.
- Bloom, Howard. 2012. The God Problem: How a Godless Cosmos Creates. New York.
- Boas, George. 1936. “Presuppositions of Aristotle's Physics”, The American Journal of Philology 57, No. 1: 24 -32.
- Boyer, Carl B. 1945. “Quantitative Science without Measurement: The Physics of Aristotle and Archimedes”, 60, No. 5: 358-364.
- Broadie, Sarah. 2004. “De Generatione et Corruptione I 4: Disntinguishing Alteration. In F.A. de Hass & J. Mansfeld (eds.), Proceedings of the XVth Symposium Aristotelicum: 123-150. Osford.
- Byrne, Christopher. 2001. “Matter and Aristotle's Material Cause”, Canadian Journal of Philosophy 31, No. 1: 85-111.
- Byrne, Patrick H. 1997. Analysis and Science in Aristotle. Albany.
- Cantu, Paola. 2010. “Aristotle's prohibition rule on kind-crossing and the definition of mathematics as a science of quantities”, Synthese 174, No. 2: The Classical Model of Science I: A Millenia-old model of Scientific Rationality: 225-235.
- Carteron, Henri. 1923. La Notion de Force dans le Systeme d'Aristote. Paris.
- Charlton, W. 1970. Aristotle's Physics Books I and II. Oxford.
- Code, Alan. 1986. “Aristotle's Investigation of a Basic Logical Principle: Which Science Investigates the Principle of Non-Contradiction?”, Canadian Journal of Philosophy 16, No. 3: 341-357.
- Cook, Kathleen C., “The Underlying Thing, the Underlying Nature and Matter: Aristotle's Analogy in Physics I 7”, Apeiron: A Journal for Ancient Philosophy and Science 22, No. 4: 105-119.
- Daney, Russell. 1978. “On Some of Aristotle's Second Thoughts About Substances: Matter”, The Philosophical Review 87, No. 3: 372-413.
- de Santillana, Giorgio and Reiche Harald. 1959. Aristotle and Science: A Critical Controversy. Boston.
- Demos, Raphael. 1946. “Aristotle's Conception of Matter”, The Classical Weekly 39, No. 17: 135-136.
- Downy, Glanville. 1963. “Aristotle and Modern Science”, The Classical World 57, No. 2: 41-45.
- Drabkin, Isreal E. 1938. “Notes on the Laws of Motion in Aristotle”, The American Journal of Philology 59, No. 1: 60-84.
- Einarson, Benedict. 1936. “On Certain Mathematical Terms in Aristotle's Logic: Part I”, The American Journal of Philology 57, No. 1: 33-54.
- Falcon, Andrea. 2005. Aristotle and the Science of Nature: Unity without Uniformity. Cambridge.
- Ferejohn, Michael T. 1980. “Aristotle on Focal Meaning and the Unity of Science”, Phronesis 25, No. 2: 117-128.
- Fine, Kit. 1992. “Aristotle on Matter”, Mind, New Series 101, No. 401: 35-57.
- Gill, Mary Louise. 1980. “Aristotle's Theory of Causal Action in "Physics" III 3”, Phronesis 25, No. 2: 129-147.
- Grene, Marjorie. 1974. “Is Genus to Species as Matter to Form? Aristotle and Taxonomy”, Synthese 28, No. 1: 51-69.
- Hakim, Joy. 2004. “THE STORY OF SCIENCE: Aristotle Leads the Way”, Science Scope 28, No. 3, The History & Nature of Science.
- Hankinson, R.J. 1998. Cause and Explanation in Ancient Greek Thought, Oxford: Oxford University Press.
- Hintikka, Jaako. 1966. “Aristotelian Infinity”, The Philosophical Review 75, No. 2: 197-218.
- ____________. 1980. “Aristotelian Axiomatics and Geometric Axiomatics,” in Proceedings of the 1978 Pisa Conference on the History and Philosophy of Science: 133-144.
- Hussey, E. 1991. “Aristotle on Mathematical Objects,” Apeiron, 24 (4): 105-134.
- Irwin, Terence H. Aristotle's First Principles. Oxford: Clarendon Press.
- Jones, Barrington. 1974. “Aristotle's Introduction of Matter,” The Philosophical Review 83, No. 4: 474-500.
- Jones, Joe F. III. 1983. “Intelligible Matter and Geometry in Aristotle,” Apeiron: A Journal for Ancient Philosophy and Science 17, No. 2: 94-102.
- Jope, James. 1972. “Subordinate Demonstrative Science in the Sixth Book of Aristotle's Physics”, The Classical Quarterly 22, No. 2: 279-292.
- Katz, Joseph. “Aristotle on Velocity in the Void (Phys. D, 8, 216 a 20)”, The American Journal of Philology 64, No. 4: 432-435.
- Kelsey, Sean. 2006. “Aristotle "Physics" I 8”, Phronesis 51, No. 4: 330-361.
- Kerr-Lawson, Angus. 2003. “Santayana on the Matter of Aristotle”, Transactions of the Charles S. Pierce Society 39, No. 3: 349-371.
- Kirkland, Sean. 2014. “Dialectic and Proto-phenomenology in Aristotle's Topics and Physics,” Proceedings of the Boston area Colloquium in Ancient Philosophy, vol. 29, No. 1: 185- 213.
- Kneale, W. & M. 1971. The Development of Logic. London, Oxford.
- KOUREMENOS, THEOKRITOS. 1996. “Aristotle's Mathematical Matter and Eudoxus' Proportion Theory”, Wiener Studien 109: 55-85.
- Lang, H.S. “Aristotle's Immaterial Mover and the Problem of Location in "Physics" VIII”, The Review of Metaphysics 35, No. 2: 321-335.
- Lear, Jonathan. 1982. “Aristotle's Philosophy of Mathematics,” Philosophical Review XCI (2): 161-192.
- Lee, H.D.P. 1935. “Geometrical Method and Aristotle's Account of First Principles,” Classical Quarterly 29: 113-24.
- Lennox, James G. 1984. “Marjorie Grene, Aristotle's Philosophy of Science and Aristotle's Biology”, Proceedings of the Biennial Meeting of Philosophy of Science Association 1984, Volume Two: Symposia and Invited Papers: 365-377.
- Lewis, Frank. 2011. “"Predication, Things, and Kinds in Aristotle's "Metaphysics""”, Phronesis 56, No. 4: 350- 387.
- ___________. 1991. Substance and Predication in Aristotle. Cambridge.
- Loux, Michael J. 1979. “Form, Species, and Predication in Metaphysics Z, H, and Theta,” Mind 88: 1-23.
- Luyten, N. 1963. “Matter as Potency,” in E. McMullin (ed.), The Conccept of Matter in Greek and Mediaeval Philosophy: 106-107.
- Mackinnon, M. 1965. “Aristotle's Conception of Substance,” in R. Bambrough (ed.), New Essays on Plato and Aristotle: 195-196.
- Maziarz, Edward A. and Greenwood, Thomas. 1968. Greek Mathematical Philosophy. New York.
- McGowan, Daryl. 1992. “The Metaphysical Science of Aristotle's "Generation of Animals" and Its Feminist Critics”, The Review of Metaphysics 46, No. 2: 307-341.
- McKirahan, Richard D. 1992. Principles and Proofs: Aristotle's Theory of Demonstrative Science. Princeton, New Jersey.
- Modrak, D.K.W. 1989. “Aristotle on the Difference between Mathematics and Physics and First Philosophy”, Apeiron: A Journal for Ancient Philosophy and Science 22, No. 4: Nature and Knowledge and Virtue: Essays in memory of Joan Kung: 121-139.
- Mohan, Matthen and Hankindon, R.J. 1993. “Aristotle's Universe: Its Form and Matter”, Synthese 96, No. 3, Logic and Metaphysics in Aristotle and Early Modern Philosophy: 417-435.
- Mueller, Ian. 1969. “Euclid's Elements and the Axiomatic method,” The British Journal for the Philosophy of Science 20, No. 4: 289-309.
- __________. 1970. “Aristotle on Geometrical Objects,” Archiv für die Geschichte der Philosophie 52 (2): 156- 171.
- Page, Carl. 1985. “Predicating Forms of Matter in Aristotle's "Metaphysics"”, The Review of Metaphysics 39, No. 1: 57-82.
- Pettigrew, Richard. 2009. “Aristotle on the Subject Matter of Geometry” Phronesis 54, No. 3: 239-260.
- Preus, Anthony. 1970. “Science and Philosophy in Aristotle's "Generation of Animals"”, Journal of the History of Biology 3, No. 1: 1-52.
- Rav, Yehuda. 2008. “The Axiomatic Method in Theory and Practice,” Logique et Analyse, Nouvelle Serie 51, No. 202: 125-147.
- Rihill, T.E. 1999. Greek Science. Oxford, New York.
- Robinson, H.M. 1974. “Prime Matter in Aristotle”, Phronesis 19, No. 2: 168-188.
- Ross, W.D. 1924. Metaphysics. vols. I &II. Oxford: Oxford University Press.
- Russo, Lucio. 1996. The Forgotten Revolution: How Science was Born in 300 BC and Why It had to be Reborn. Berlin, New York.
- Sachs, Joe. Aristotle's Physics: A Guided Study. New Brunswick and London: Rutgers University Press.
- Scharle, Margaret. 2009. “A Synchronic Justification for Aristotle's Commitment to Prime Matter”, Phronesis 54, No. 4/ 5: 326-345.
- Solmsen, Friedrich. 1961. “Misplaced Passages at the End of Aristotle's Physics”, The American Journal of Philology 82, No. 3: 270-282.
- Sterling, Donna R. 2009. “From Aristotle to Today: Making the History and Nature of Science Relevant”, Science Scope 32, No. 5: 30-35.
- Studtmann, Paul. 2007. “Aristotle, Science and the Plenitude of Being”, Apeiron: A Journal for Ancient Philosophy and Science 40, No. 3: 245-266.
- Suppes, Patrick. 1974. “Aristotle's Concept of Matter and Its Relation to Modern Concepts of Matter”, Synthese 28, No. 1, On Aristotle's Philosophy of Science: 27-50.
- Sylla, Edith Dudley. 1979. “The a Posteriori Foundations of Natural Science: Some Medieval Commentaries on Aristotle's "Physics", Book I, Chapters 1 and 2”, Synthese 40, No. 1: 147-187.
- Taisbak, C.M. 2002. “Euclid's Elements 9.14 and the Fundamental Theorem of Arithmetic,” in Science and Mathematics in Ancient Greek Culture. C.J. Tuplin and T.E. Rihill (eds). Oxford and New York.
- Upton, Thomas V. 2004. “Truth vs. Necessary Truth in Aristotle's Sciences”, The Review of Metaphysics 57, No. 4: 741-753.
- Wilson, Malcolm. 2000. Aristotle's Theory of the Unity of Science. Toronto, Buffalo, London.