Life and Works

Euclid was a geometer, mathematician and perhaps a Platonist [i] whose floruit occurred between 325 and 250 B.C., but what information scholars posses about Euclid's life is at best unreliable. He likely taught in Alexandria Egypt during the reign of Ptolemy Soter (323-285 B.C.) and has been considered a great schoolmaster as well as a man of the utmost honesty. [ii] The most prominent mathematician of the Graeco-Roman period, he is best known for his work Elements, and largely relegated to the status of geometer. Other preserved works are Optica, Catoptica, Sectio Canonis and Phaenomena, all of whom together demonstrate that Euclid knew the whole range of mathematics and mathematical topics of his day. [iii] Indeed he seems to have culminated all that came before him in his work. Though he covered other material in other works, his Elements is far from simply geometry. Euclid's aim in Elements was to make geometric proofs using only a compass and a ruler and to establish a theory of numbers; thus with limited tools, he produced a highly sophisticated work. iv Geometry was meant to be simple at its root and therefore beautifully structured, which reflected the Greek sense of virtue in general. Euclid may have made certain proofs on his own, but he also compiled the work of earlier thinkers into Elements, proving their theories perhaps more vigorously. Thinkers were not obliged to cite sources in the way modern scholars do, and so Elements is perhaps the legitimate culmination of geometry and some mathematics, but it is not the work of a titanic genius, as may be supposed. It is at least the work of a genius compiler who proved theories that already existed, theories that had not been proven as vigorously and in conjunction with one another. Make no mistake; Elements is a work of genius. Yet, Euclid's contribution must be put into perspective. Not only is he not responsible for all of the proofs in Elements, but he may not be responsible for the majority of them. There is no way to extract fully what Euclid adds to what already existed. Still, scholars have some idea who contributed to his work and basically what that constituted. One must think of Elements as an enormously successful textbook, [v] sometimes mistakenly giving readers the impression that Euclid discovered a titanic multitude of proofs and truths.

The method Euclid employs is an axiomatic one, [vi] and that means he makes use of fundamental, atomic propositions that he uses to build a very powerful system, beginning with the easier material and progressing methodically into complicated proofs. [vii] Atomic propositions are statements considered to be self-evident, like the old metaphor of building blocks. Once one acknowledges these statements as true the rest of Euclid's system follows because he reasons in a deductive manner. His proofs are composed of long combinations of accepted truths and logical connections. These connections make propositions. In fact, Euclid makes a proof for one proposition and uses that as an element for another, later proof. His way of making an argument [viii] is thus thorough and meticulous, sometimes seemingly tedious, but all of the pieces need to be arranged in order to build a strong edifice. [ix] And his construction is so strong that it lasted until late in the nineteenth century when alternate geometries gained traction in the academic community. [x] One anecdote [xi] from the ancient world speaks to the rigor and potency of Euclid's work. He was asked by Ptolemy the king if there was not a shorter road to geometry than through his Elements. His response was that there is no royal road to geometry. Another anecdote speaks to what one may obtain from studying geometry. Euclid was asked by one of his students what profit there is to gain from the study of geometry. He called a slave and told him to give the student a coin or two, since he must profit from what he learns. Euclid's Elements may seem sometimes tedious, but it is beautiful and true, profitable and useful in itself – powerful indeed.

It is appropriate here to acknowledge the work of the thinkers and scholars on whose work Euclid built his famous text. They are, after all, responsible for his success in a most significant way. Elements is composed of thirteen books, [xii] beginning with simple proofs and graduating to more difficult ones. Euclid drew from Aristotle at least one of his most fundamental axioms, but he may have used a great deal more. [xiii] Hippocrates of Chios whose floruit comes c. 440 B.C. wrote the first known Elements of geometry a century before Euclid wrote his Elements. Hippocrates attempted to “square the circle” and portions of his Elements have been preserved in the work of Proclus, a Greek philosopher. Perhaps the whole idea of a book of geometric elements came from Hippocrates. The Pythagorean Theatetus who lived from 417-369 B.C. contributed a great deal of material from which Euclid wrote the later books of his treatise: XI–XIII three-dimensional figures, XI intersections of planes, lines, and parallelepipeds (solids with parallel parallelograms as opposite faces), and XIII the construction of the five regular Platonic solids (pyramid, cube, octahedron, dodecahedron, icosahedron) in a given sphere. Eudoxus of Cnidos whose floruit occurred c. 395/390–342/337 B.C. was another significant contributor. Book XII of Euclid's Elements consists in part of Eudoxus’s method of exhaustion, which Euclid used to prove that areas of circles are to one another as the squares of their diameters. Also Euclid used Eudoxus' work to prove that the volumes of spheres are to one another as the cubes of their diameters.

First Principles

Book I of Elements lists twenty-three definitions, five unproved axioms and five more unproved assumptions. Euclid called the axioms “postulates” and the unproved assumptions “common notions”, but it is best to define our terms in order to be as orderly as possible. An axiom is a self-evident truth about something, an assertion that everyone agrees is true. It needs no proof. The term comes from the Greek axioma, which means “worthy.” A postulate is simply asserted as true but it lacks the self-evident nature of an axiom. It is as if Euclid were to say that he wants his readers to take this assertion as true, and he employs that assertion as a truth. There is no need to prove a postulate, though perhaps a proof will make a postulate stronger. These assertions are sometimes intuitive, and sometimes simply asserted for purposes of making a proof, but without doubt they are necessary as atomic elements of each line of reasoning. We will see that there are some proofs of things that we would take as truth without proof, but Euclid knew that he needed to prove every item. Again his attention to detail of this kind leads some to see his work as tedious, but the so-called tedium is quite necessary. [xiv] Many of the postulates are self-evident, but most are provable. [xv] First, here are Euclid's definitions [xvi] from book I of Elements, which make clear what terms mean what.

1. A point is that of which no part exists.

2. And a line is length with no breadth.

3. And the extremities of a line are points.

4. A straight-line is whichever one lies evenly with points on itself.

5. And a surface is what has length and breadth alone.

6. And the limits of a surface are lines.

7. A plane surface is whichever lies evenly with the straight-lines on itself.

8. And a plane angle is the bending of the lines to one another, when two lines in a plane meet one another, and are not lying in a straight-line.

9. And whenever the lines containing the angle are straight, the angle is called rectilinear.

10. And whenever a straight-line stood upon (another) straight-line makes adjacent angles (which are) equal to one another, each of the equal angles is a right angle, and the former straight line is called a perpendicular to that upon which it stands.

11. An obtuse angle is an angle greater than a right-angle.

12. And an acute angle (is) an angle less than a right-angle.

13. A boundary is that which is the limit of something.

14. A figure is that which is contained by some boundary or boundaries.

15. A circle is a plane figure contained by one line [which is called a circumference], (such that) all of the straight lines falling towards [the circumference of the circle] from one point among those lying inside the figure are equal to each other.

16. And the point of the circle is called the center.

17. And a diameter of the circle is some straight-line, drawn through the center, and terminated in each direction by the circumference of the circle, (and) whichever (straight line) also cuts the circle in half.

18. And a semi-circle is the figure contained by the diameter with the circumference cut off by it (the diameter). And (the) center of the semi-circle is the same thing as (the center of) the circle.

19. Rectilinear figures are the ones (figures) contained by straight-lines: trilateral figures (being) the ones contained by three straight-lines, quadrilateral by four, and multilateral by more than four.

20. And of the trilateral figures, an equilateral triangle is the one having three equal sides, an isosceles (triangle) the one having only two equal sides, and a scalene (triangle) the one having three unequal sides.

21. And further of the trilateral figures, a right-angled triangle is the one having a right angle, an obtuse-angled (triangle) the one having an obtuse angle, and an acute-angled (triangle) the one having three acute angles.

22. And of the quadrilateral figures, a square is the one which is right-angled and equilateral, a rectangle the one which is right-angled but not equilateral, a rhombus the one which is equilateral but not right-angled, and a rhomboid that having opposite sides and angles equal to each another which is neither right-angled nor equilateral. And let quadrilateral figures besides these be called trapezia.

23. Parallel lines are straight-lines which, being in the same plane, and being extended to infinity in each direction, meet with one another in neither (of these directions).

Notice that Euclid is making clear what he means when he uses specific terms that could themselves be defined in other ways, sometimes differently nuanced. So, definitions are not accepted truths as much as they are ways of using specific terms. Also, notice that a point is a most fundamental unity, or whole in that it is “that of which no part exists.” It is atomic and number as a unit is also this uncut part of reality. It has no length or breadth because it is simply at some spot that technically cannot be measured. A point is a rendering of a whole or unity, which is for Euclid likened to number. In fact, Euclid defines number in a similar manner, and from this definition he creates a spatial extension of number. So, in some sense he is a Pythagorean influenced strongly by Plato. Second, here are the postulates from Book I of Euclid's Elements. Euclid writes “let the following be postulated.”

1. To draw a line from any point to any point.

2. To produce a finite straight line continuously in a straight line.

3. To draw a circle with any center and distance.

4. That all right angles are equal to one another.

5. That, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if extended to infinity, meet on that side of which are the angles less than the two right angles. [xvii]

And here are the axioms from Book I of Euclid's Elements. Euclid calls them “common notions.”

1. Things which are equal to the same, or to equals are also equal to one another.

2. If equals be added to equals, the sums are equal.

3. If equals be taken from equals, the remainders are equal.

4. Things which coincide with each another are equal to each another.

5. The whole is greater than the part.

The definitions, postulates and axioms function together as the foundation of Euclid's axiomatic proofs, but it is important to note that each book – with the exceptions of 8, 9, 12 and 13 – has definitions. One will remember that Pythagoras talks about the relationship of sections on a chord that produce a similar sound. The ratio of ½ is an eighth, but one must begin at a particular point in order to determine the ratio. One cannot begin at 0. Once the point on the line of the chord is determined, one is able to determine where are the other eighth tones because the point on the line that lies a specific distance from another point has a similar sound. Yet, one must begin at some point in order to make the determination. Beginning at 0 leaves no possibility to make a ratio because there is no measure. In other words, ½ of zero is zero, so one moves to no other point on the chord. The definitions, postulates and axioms of Euclid operate in a similar fashion in his Elements. They supply the reference points for an analysis of figures in two and three-dimensional space, a starting point that allows the system to begin and founds it. Notice as well that such systems of reasoning are relative. They, like all reasoning, need a reference point from which to understand the system. Otherwise, like beginning at zero there is nothing from which one proceeds.

Euclid's system of measurement and logic produces quite strong proofs of the certainty of many geometric figures and shapes, though some moderns have found fault with his methods and proofs. His method is fully deductive and it is not until the nineteenth century that logicians and geometers realize they are able to begin a new system of reasoning by beginning at different reference points. Euclid's proofs were taken as certain for that long, and it is important to remember that his proofs are not proofs in the sense that they make reasoned hypotheses and later prove them with empirical evidence in the traditional sense. [xviii] They are more pure reasoning and “prove” something in the sense that they demonstrate how specific aspects of figures and shapes can be realized with mathematical precision and logical certainty. A proof will demonstrate that one can be certain about what amounts to outlines of objects encountered in the universe. They demonstrate precise measurement and relationships between lines, points and space. There are no more clear arguments, though perhaps Euclid's geometric system is not the only way to measure figures.

Causation, Argumentation and Cosmology

Book I of Elements proves elementary theorems about triangles and parallelograms, culminating in Euclid's proof of the Pythagorean theorem. Book I also contains the famous pons asinorum, [xix] beyond which good students may pass but past which bad students cannot. Recall that Aristotle's syllogisms individually are three statements long. Each syllogism may be coupled with other syllogisms in order to form longer arguments, but the fundamental arguments are composed of three lines. Euclid's arguments may be three lines, but they may also be much longer, and that longer proof may become an element of another, more sophisticated, argument. Our concern will be showing how the various proofs can be used together. We concentrate on Book I, which culminates in Euclid's proof of the Pythagorean theorem. His proof of the Pythagorean theorem is itself comprised of propositions 4, 14, 31, 41 and 46.

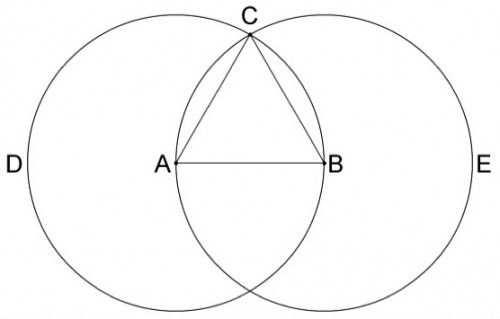
Euclid begins Book I by demonstrating how it is possible to create an equilateral triangle: Book I, Proposition 1

On a given finite straight line to construct an equilateral triangle. Let the given straight line be AB. There is need then to construct an equilateral triangle on the straight line AB. Let the circle BCD be drawn with center A and radius AB [Post. III], and again let the circle ACE be drawn with center B and radius BA [Post. III]. And let the straight lines CA and CB have been joined from the point C where the circles cut each other to the points A and B (respectively) [Post. I]. And because point A is the center of the circle CAE, BC is equal to BA [Def. 1.15]. But it was shown that CA is equal to AB. Thus, CA and CB are both equal to AB.