Plato

Life and Works

Plato was an aristocratic Athenian philosopher and student of Socrates and of Cratylus who lived circa 427-347 B.C. His mammoth contribution to western culture and thought cannot be overestimated. Responsible for foundation questions about metaphysics, ontology, politics, practical wisdom and other issues, Plato demonstrates a depth of interest and knowledge rarely seen in philosophers and thinkers in general. He wrote dialogues, which largely are narrative discussions between his philosophical hero Socrates and Athenian aristocrats, many times young men. These dialogues are part of his method, which is fundamentally a continued questioning without the expectation of an absolute answer. Plato is one of the only thinkers of the ancient world whose work survives practically extant, so great was his reputation and influence. He was not what we may call a physicist, and so his main preoccupation was not the material composition of the universe.[i] He did, however, write a dialogue specifically addressing the issue of the genesis of the universe and its “likely” physical composition. It is necessary to review Plato's conception of the origin and composition of material reality in his Timaeus, but of great concern for scientific inquiry is his method of questioning, refuting and answering – his elenchus – which permeates his thinking and is found in his dialogues. In Timaeus is located his account of the universe's genesis [ii] and in Meno one finds a way of reasoning whose foundation remains an integral part of scientific inquiry.

First Principles

Timaeus reveals what Plato considered to be “probably the case” of the composition of material reality. Yet, Plato disdained matter and material explanations for concepts, things and objects.[iii] He believed in a deeper aspect of reality than matter because matter comes to be, brings itself to fruition and falls away. It is thus unstable. Things that come to be are for Plato unreliable examples of what things really are. He directed his methods at understanding a metaphysical aspect of reality that infused becoming with being, which is to say that the most fundamental aspects of reality are not the things we see, touch, hear etc., but rather they are the things that exist always and have no movement; they are being. This being we cannot directly sense, but the mind connects with being through reason:

The one thing truly grasped by the mind with reason always exists in the same way, and another thing again [grasped by] belief with unreasoning perception is a matter of opinion, always coming to be and passing away but never truly existing. (Plato, Timaeus 28a)[iv]

In the majority of Plato's dialogues there are at least two interlocutors who talk to one another, engaging a topic with questions and answering, but Plato's Timaeus is largely a monologue of a single character explaining how the universe arose and what is its material and metaphysical composition. The awareness that it is a monologue is important in that Plato likely treated the topic of the material composition of the universe with a bit more than a little distaste, and so there is no dialogue [v] about physics. Timaeus explains gargantuan topics with almost no questions and insufficient description, which is not to say that there is no depth to the dialogue. Again, Plato's interest resided in what was for him more real, a reality accessible to the mind and a fundamental but almost hidden part of material becoming.[vi] Still, Plato discussed material processes, but with respect to his metaphysics of being and becoming. The material universe for Plato is made from earth and fire because the characteristics of those two elements seem to enable sensation and thus perception:

...the seen and the touched things that come to be must be in body-form, but nothing would ever come to be seen apart from fire, nor touched without some solid, nor solid without earth. Setting out to organize from fire and earth did the god make all bodies. (Plato Timaeus 31b).

Earth and Fire make up parts of the universe, but the universe itself must be bound together, and its bind resides for Plato in proportion, a naturally mathematical relationship:

...it isn't possible to combine two things well by themselves without a third; some unifying bond is needed in the middle of both. The finest of bonds is the one that makes the things bound together and itself one as much as possible, and naturally mathematical proportion accomplishes this in the best way. For whenever of three numbers that either have mass or (mathematical) powers the middle term between any two of them is such that what the first term is to it, it is to the last, and, in reverse, what the last term is to the middle, it is to the first, then, since the middle term comes to be both first and last, and the last and the first again both turn out to be middle terms, all things in this way from necessity will happen to be the same things, and all the same things shall have come to be one in relation to one other. (Plato Timaeus 31c-32a).

We must remember that for Plato, like for Euclid later, the relationship that exists between numbers and spatial extension has a greater significance than mere measurement, which is how moderns understand that relationship. How things have cohesion is that part of objects and creatures that bonds them; it is mathematical and because spatial extension and number are intimately related – which is to say that proportion makes things one and thus unified – proportion is a genuine bond in material things. Another way to understand what is happening in Timaeus is to see that being is the part of reality, for Plato, that does not change. It is static and it is the foundation for the things that are not static, things that change. Being is un-cuttable and, as eidoi (Forms), provides a basis for things that come-to-be. A mathematical equation is a truth that will exist no matter if there is a manifestation of it or not. A circle will always have as part of its measurement π (ratio of a circle's diameter to its circumference) or πr² (area of a circle). There is something in the mathematical equation that goes beyond mere happenstance, and its foundation is being (Forms) that is the permanent aspect of the universe. So, a mathematical equation that demonstrates a bond between two numbers really is bond itself, a more permanent bond than physical things engage. Such being makes number generative in that the bond between elements makes things. Number is more real for Plato than things that become and so proportion creates a most significant bond. One example is that cubes, or a number multiplied by itself three times, are considered to be solids. We will see that Plato's elements themselves are comprised of shapes that themselves have proportions because this proportion is needed for the bond:

Some things have come to be bound up with it itself and are solid-formed, but one term never fits together solids, but two middle terms do. In this manner the god having set water and air between fire and earth [and] having worked out as much as possible the same proportion for each to each – so that what fire is to air, air is to water, and what air is to water, water is to earth – he bound together and organized a sky both visual and tangible. (Plato, Timaeus, 32b).

The elements themselves have a mathematical relationship to one another that is similar to the proportion just described. Additionally, material reality is for Plato atomistic. One says “atomistic” because atomists, in addition to believing in uncut and uncuttable bits of reality, believed in a void that Plato did not and Plato's atoms have parts. In fact, a significant part of the atomist doctrine was matter combined with void in different ways, but Plato believed that matter is composed of tiny, imperceptible bits of physical substance:

It is necessary to think of these things as so small, so that, due to their small size, each of each kind individually is not visible to us. When, however, many of them are assembled together, the mass of them are seen. (Plato, Timaeus, 56b-c).

Gaps and density make chemical processes possible:

Neither fire nor air will melt masses of earth, because naturally they [fire and air] are things of smaller nature than the composition of the gaps in the earth. They pass through the wide gaps of earth, not being constrained, leaving it continuous and unmelted. But since the parts of water are greater by nature, forcibly making an outlet for themselves, and loosening it [earth] they melt the earth. For water alone in this way loosens earth not compressed by force, but nothing but fire dissolves compressed earth, because an inside-path is left behind by nothing except fire. And fire alone disperses the most forcibly concentrated water, yet both fire and air scatter a looser state of water. Air enters the gaps, and fire breaks up the triangles. Nothing loosens air condensed by force except along [its] elements, and fire alone melts down [water] not condensed by force. (Plato, Timaeus, 60e-61a).

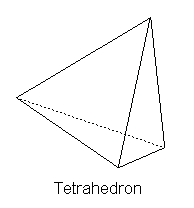
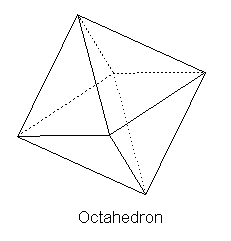
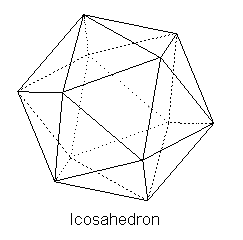
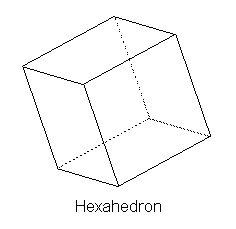
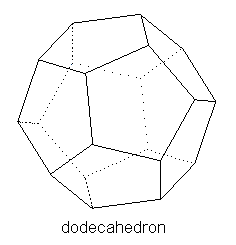
The logic of Plato's chemical process seems to be that of gaps between minuscule bits of matter functioning together with the size and shape of the elements. When there exist gaps through which elements can pass, there is a chemical mixture, or perhaps we may call it a chemical reaction. These tiny bits of matter interact through these gaps, yet there is no void, or complete lack of being, anywhere in the Platonic universe; only a kind of Parmenidean being exists. These bits of material, mathematical reality that Plato did accept themselves were composed of aspects of reality more fundamental than becoming. Plato accepted the four elements of Empedocles – earth, air, fire and water – but only as atomistic geometric shapes.[vii] These shapes are themselves elements too small to perceive with the senses, but in larger groupings they become visible: Fire elements took the shape of the tetrahedron. Earth elements took the shape of the cube. Air elements took the shape of the octahedron. Water elements took the shape of the icosahedron. The overall universe was shaped like a dodecahedron:

To earth let us [designate] cube because earth is the least moving and most moldable of the four kinds of bodies, and it is most necessary that this sort of thing has come about having the most steadfast faces. The face of the initially postulated triangles that belongs to the ones having equal sides is more steadfast than the one that belongs to triangles having unequal sides, and the surface composed of the two triangles, the equilateral quadrangle [the square], holds its position with greater stability than does the equilateral triangle, both in their parts and on the whole. ...and of the solid figures that are left, we designate the form most difficult to move to water, to fire the easiest [form] to move, and the middle [form] to air. The smallest body is fire's, the largest water's, and the middle one air's; the sharpest body is fire, the second sharpest is air, and the third sharpest water. (Plato, Timaeus, 55d-56a).

The atomistic and geometric shapes were used up in the construction of the universe:

The construction of the universe used up each of the four [elements], for from fire and all of water and air and earth the one who set it up put it together, having left behind no part of anything nor any power. He intended these things: first, that it be a living whole as much as possible and complete from completed parts; next, it should be one, so as nothing be left over from which another one of this sort could come to be; and further that it should be ageless and lacking in disease. He observed that heat or cold or anything else that has strong powers surrounds a composite body from outside and assails it, it destroys the body prematurely, bringing diseases and old age upon it and makes it waste away. (Plato, Timaeus, 32c-33a).

The atomistic shapes themselves were composed of isosceles and scalene right-angled triangles:

First that fire, earth, water and air are bodies is clear in some degree to all. Every form of body has depth. There is every necessity that surface surrounds depth by nature, and a linear surface is put together from triangles. All triangles are derived from two triangles, each having one right angle and two acute angles. One of these triangles [isosceles right-angled triangle] has on each side a part of a right angle that is divided by equal sides; the other [scalene right-angled triangle] has unequal parts of a right angle on each side divided by unequal sides. This we posit as the source of fire and of the other bodies, furnishing them according to the likely account of necessity. Principles of these [triangles] a god [alone] knows, and whoever among human beings is dear to him. (Plato, Timaeus, 53c-d).

In fact, the fundamental shape that gave rise to material reality was the triangle, whose different shapes composed the Platonic solids that interacted on a minute scale. The geometric atoms are the atomic universe and the triangles are the subatomic universe in the modern sense. These fundamental triangles sometimes broke one another down and sometimes built upon one another, depending on the kinds of triangles involved:

Four kinds of bodies come to be from the [right-angled] triangles we have selected; three of those come from triangles possessing unequal sides, but the fourth alone is fitted together from isosceles triangles. Certainly not all of them, breaking up from many small bodies and turning into each other, are able to become many small bodies [converting] into a small number of large bodies and the reverse. Three are able to do this. For all three come about from a single [type] of triangle; when the larger bodies have been broken up, many small [bodies] will be put together out of the same [triangles], taking on shapes appropriate for them. And again, when many small bodies are broken up into their triangles, having come to be one great mass number, they may come to fruition as one single form. (Plato, Timaeus, 54b-d).

Plato had his own subatomic theory: two kinds of right triangles were the base units of all elements. These had three legs that were never separated. One kind of triangle was the isosceles triangle formed by cutting a square in half: 1, 1, √ 2. Another was formed by cutting an equilateral triangle in half: 1, 2, √ 3. He constructed the first four solid faces with these triangles.

One cannot make a pentagon from these triangles, but other sources indicate that Plato thought a pentagon ought to be constructed like the five-sided shape above. The triangle face consisted of six triangles, the square face of four and the pentagon of thirty triangles. Because the tetrahedron possessed four sides it was composed ultimately of 24 triangles, the octahedron of eight sides 48 triangles and the icosahedron with twenty sides of 120 triangles. These triangles were of the 1, 2, √ 3 kind. The hexahedron or the cube having six sides was composed of 24 triangles of the 1, 1, √ 2 kind. The dodecahedron consisted of 360 triangles because of the complicated manner in which each face was composed. One can see how elements break down and reform, if the most fundamental, immutable particles are the triangles. These elements interact with one another and so account for changes in material reality. [viii] In this manner Plato gives an ancient account of chemistry, the elements themselves interacting with one another in fairly predictable ways.

When earth encounters fire and is broken up by its sharpness, it may drift about–either having happened to break up within fire itself, or within a mass of air or water – to a given point its parts happen upon it somewhere, they [the parts] refit themselves together and become earth. For the parts of earth will never pass into another form. But water broken into parts by fire or even by air, it is possible that the parts reunite to become one corpuscle of fire and two of air. And the pieces of air, broken up from any single part that is broken up, may become two bodies of fire. And again, whenever a bit of fire is enveloped by a sizable quantity of air or water or some earth – being moved inside the ones being carried about and while resisting is overcome and shattered – then any two bodies of fire may combine to constitute one form of air. And when air is overpowered and cut to pieces, then two and one half entire forms of air will be compacted into a single, entire form of water.(Plato, Timaeus, 56c-e).

The Platonic elements are not random shapes that Plato chose. They are “the only perfectly symmetrical arrangements of a set of (non-planar) points in space.”[ix] Plato adopted his colleague Theatetus' assessment of the five shapes. The tetrahedron was composed of four composite equilateral triangles formed from the faces above, three triangles meeting at each vertex. The fourth triangle is the base formed from the meeting of the three triangles. These triangles, the tetrahedron, form fire.

Four composite triangles meeting at one vertex make a pyramid with a square at its bottom. Two of these fused at the square base become the octahedron, which is the shape with eight sides, or air.

Five composite triangles meeting at one vertex make a twenty-sided shape when they are joined with other triangles that form sets of triangles meeting at each vertex. The shape thus produced is the icosahedron, or water.

It is not possible to construct perfectly symmetrical solids by adding more triangles. The shapes become irregular to the point of being useless to ancient Greeks. In other words, adding another triangle does not produce a finite solid, and the ancient Greeks would not have believed an infinite solid could be a fundamental part of the composition of the universe. Three composite squares fused at one vertex form a solid angle, and if three more squares are added to those three, a hexahedron, or cube, arises.

No triangle that forms the side of a square can be equilateral, so as we have seen the square is composed of triangles that differ from the other elements: 1, 1 √2. The square is the shape of the element earth and because its triangles are not the same as in the other elements, earth elements cannot exchange their triangles with the other elements. Three composite pentagons meeting at one vertex make one part of a twelve-sided figure, if the pentagons are arranged such that twelve pentagons make a solid. The resulting twelve-sided shape is the dodecahedron, or the shape of the universe.

Not insignificant is the fact that these shapes are in a sense proportionate to one another. The icosahedron and the dodecahedron are duals of one another. In other words, while the icosahedron has twenty faces and twelve vertices the dodecahedron has twelve faces and twenty vertices. Having six faces and eight vertices and then eight faces and six vertices respectively, the cube and the octahedron are duals of one another. The tetrahedron is the dual of itself. Plato's requirement that the universe has proportion seems to have been met in the relationship of these elemental shapes to each other. We will see below that geometric shapes are similar in kind to Platonic eidoi, whose more fundamental reality is both unchanging and eternal. In other words, the elements, being essentially shapes, themselves reduce to mathematical aspects. These mathematical aspects were themselves non-material, and thus the most fundamental aspect of material reality was itself immaterial. In other words, the very material atoms in which Plato believed have at their root an immaterial reality. They are being (Forms) that the mind reasons.[x]

Causation and Cosmology

The deity that acted as a catalyst for being to come to be was a demiurge,[xi] or a kind of false god. He believed himself to be the creator of the universe, but he merely made use of already-existing perfect models to compose its overall order:

[The universe] has come to be. For it is both visible and tangible and it has a body – and all things of this kind are perceptible, and perceptible things are grasped by opinion with sense perception. Again we say that for what comes to be must come to be through some cause. ...Which of the two models did the maker use when he completed [the universe]? Was it the one possessing the same things and being always as it is, or the one that has come to be? If this universe is beautiful and its craftsman good, then it is clear he looked at the eternal model. But if what is not right to say is the case, [then he used] the one that came to be. Now truly it is clear to all that [he used] the eternal model, for [our universe] is the most beautiful of all the things that have come to be, and the best of causes is its craftsman. (Plato, Timaeus, 28b-29a).

The demiurge shaped the universe into a sphere.

And he gave to it [the universe] a shape appropriate and natural to what it was. That is the appropriate shape for a living thing that is about to contain within itself all shapes there are on account of which it became sphere-formed, its center equally holding distance from its extremes in all directions, turned round in a circle. It is the most complete and most like itself of all shape, which he gave to it because he believed that likeness is infinitely more excellent than unlikeness. (Plato, Timaeus, 33b).

The universe was itself a living organism.

...out of the things naturally seen nothing without a mind on the whole will ever be more beautiful than anything having a mind on the whole, and it is impossible that mind came about from it separate from soul. On account of this reasoning [the demiurge] crafted the whole [universe] having set mind in soul and then soul in body so that [the universe] would be as naturally beautiful as possible and so that he completed the best work. In this manner then, according to a likely account, there is need to speak of this as a living universe both en-souled and with mind, and truly through the forethought of the god it came to be. (Plato, Timaeus, 30b-c).

Fundamental aspects of the universe are Forms – accessible through reason.[xii]

If mind and true opinion are two kinds [of things], then absolutely these things exist by themselves–Forms unperceived by us, [but] being objects of mind alone. But if...true opinion differs in no way from mind, then however many things we perceive through the body must be acknowledged as the most steadfast things that exist. Those two must be spoken of, on account of them having come to be separate and being dissimilar. The one of them [mind] comes about for us through instruction, and the other [true opinion] by persuasion. Mind always comes about with a true reasoning while [true opinion] comes about without reason. And the one [mind] is unmoved by persuasion, and the other [true opinion] is open to persuasion. (Plato, Timaeus, 51d-e).

They are eternal and unchanging realities that existed prior to the formation of the order of things, what the demiurge used to create the living and en-souled universe:

The god...gave priority and seniority to the soul both in its coming to be and in virtue, as the master of the body ruling over it [the body] as one ruled for its own good. He established it from these things and in this manner: Between indivisible and always changeless being and what [being-becoming] is divisible and comes to be in the bodies, he mixed a third form of being in the middle of the other two. And as far as the constitution of the Same and of the Different he established things in the same way in the middle of the indivisible [things] and of the divisible, somatic parts. And having taken the three things he mixed them together into a uniform kind, fitting together by force the nature of Different, which resisted mixing, into the Same. Having mixed these two with Being from three he had made one, [and] again he divided the whole into as many parts as was fitting, each part itself mixed from the Same, the Different and from Being. (Plato, Timaeus, 34c-35b).

The Forms, or eidoi, here are Same, Difference and Being, but one can easily imply a Platonic form into the triangles that compose the elements and thus material reality. Remember that for Plato the formulas for triangles and circles exist even though there is no manifestation of them. The same is true of the forms (eidoi). Forms are metaphysical "arrangements" of sorts that are the things that become in the universe. One may think of them not as the spatially extended numbers of the Pythagoreans, but as fundamental, spaceless and timeless most real organizations that the becoming universe imitates. Number expresses geometric shape without an actual shaping of substance into geometric form, and in this way numeric equations are excellent metaphors for the nature of Platonic Forms.[xiii] They are similar to the equation for geometric shape. When we say that A²+B²=C², we are saying the shape without seeing it and without its manifestation as a shape. Geometric shapes, like Platonic Forms, need not become manifest in order to remain possible or even actual in a more fundamental sense of the word “actual.” In other words, no matter what becomes in the universe the Pythagorean theorem is true for certain types of triangles. No time or space or anything else needs to exist; no triangle needs to come to be in order for that calculation and a fundamental reality to be true about triangles. Similar but more fundamental is the immaterial nature of Platonic eidoi; and Same, Difference and Being are themselves eidoi, possessing a more fundamental, more real nature. So, the geometric shapes of the Platonic atoms themselves imply eidoi that are more fundamentally real than material manifestations. It is on this kind of metaphysical basis that the Platonic elements are based, and thus geometry allows Plato to make a connection between his theory of forms and his “probable account” of material, atomistic reality. These forms operate on anything and everything in the universe. Forms even create the levels of the cosmos for Plato, who believed that the revolutions of the stars and celestial bodies are eternal whereas the becoming of the realm near the earth is mortal:

Next, having sliced this whole compound in two along its length and having thrown each one middle to middle like an X [the demiurge] bent them down into one circle, binding together each half to itself end to end and to the ends of the other half at the point opposite to the one where they had been joined together. He then included them in that motion revolving in the same place in the same way, and began to make one the outer, and the other the inner circle. And he assigned to the outer movement the movement of the Same, and to the inner the movement of the Different. The one of the same he led around to the right along the side, and the different to the left along the diagonal, and he gave strength to the revolution of the Same and Similar in that he left this one alone undivided, as he divided the inner one six times, to make seven unequal circles.... (Plato, Timaeus, 36c-d).[xiv]

These circles are the celestial spheres on which the stars and other bodies rotate, creating an eternal world of the outer sphere and an inner world of mortality. Yet, if all of these aspects of the universe are immaterial at their root, then there must be something unlike a form that is the foundation for becoming. Plato realized the necessity of explaining what is it that becomes.[xv] His answer is that there is some aspect of reality, both changing and itself unstable, that allows the shapes of the triangles and the eidoi of the universe to come into being without actually being born, growing and wasting away:

[The receptacle] is perceived by the senses, begotten, always borne along, coming to be in a certain place and again perishing out of it, apprehended by opinion with perception. (Plato, Timaeus, 52b).

Since that for which an image has come to be is not at all inherent in the image, an image perpetually borne along to picture something else, on account of these things it is fitting that the image should therefore come to be in some other thing, in some way adhering to being, or else be absolutely nothing. But for that which really is the account of true precision is an aid: as long as the one is one thing and the other another, neither of them has ever come to be in the other in such a way that they at the same time will become one and the same, and also two. (Plato, Timaeus, 52c-d).

This aspect of the universe Plato called the receptacle. It was the “space” into which these models were placed and an unstable, ever-changing mass of nothing-in-itself that permitted the Forms to come to be in it, while at the same time never becoming the Forms nor being changed fundamentally by the Forms participating in it.[xvi] Some scholars think of it as matter. When one considers the ultimate reality of geometric shapes as mathematical objects, the relationship of the Platonic eidoi and the elements as material reality comes closer. The elements are mathematical and so also intermediate or similar in kind to Platonic forms, yet they come to be in the receptacle; number and mathematics then are intermediate to eidoi (forms) for Plato. The being of the universe for Plato is fundamentally immaterial and eternal and also much more real than the objects that we perceive.

Argumentation

Plato's conception of material reality is obviously not what scientists believe now, but there are aspects of his thought that survive in science. His insistence on continued questioning forms the basis of scholarly publication and thus conversation.[xvii] The manner of determining commonalities and thus comprehending patterns in nature is a fundamental part of Plato's dialogues. Plato's dialogue form was a conversation about a given topic. His philosophical hero Socrates directs the discussion on most occasions and a given dialogue possesses a specific structure. A man, usually young and aristocratic, has an interest in a specific topic. He wishes to learn from an elder, a customary practice for transferring knowledge in ancient Athens. He begins a conversation with Socrates who in turn guides him, but not in the manner as someone imparting information through a lesson. Socrates' method was to engage his interlocutor in an elenchus, which was an examination of a topic whereupon a given perspective was analyzed, perhaps refuted and then questioned. Socrates asks the young man what he thinks about a given topic – like virtue in Plato's Meno – without himself claiming he knows what it is:

But Meno...what do you yourself say virtue is? Speak and do not begrudge us so that I may have been deceived by the most fortunate falsity when I said that I had never happened upon anyone who knew, if you and Gorgias appear to know. (Plato, Meno, 71d).

When asked what is virtue, the young man usually responds confidently. Virtue seems easy to define:

But it is not difficult, Socrates, to state. First, if you wish to hear of a man's virtue, it is easy to say since this is the virtue of a man: to be able to manage the affairs of the city sufficiently, and while doing these things to do well for friends and harm enemies. And if you wish to hear the virtue of a woman, it is not difficult to relate, since there is need for her to manage the household well, preserving it and its internal affairs and listening to her husband. (Plato, Meno, 71e).

Socrates questions his interlocutor's answer.

I seem to enjoy great luck, Meno, if seeking one virtue I have found some swarm of virtue is yours. But, Meno, in keeping with this image of the swarms, if I were asking you about the being of a bee what is it, you were saying that they are many and variegated, what would you have answered me, if I asked you “Do you say that there are many and varied kinds and that they differ from each other, as far as being a bee? Or do they not differ in this way, but in some other way, like in beauty or size or some other thing of these sorts?” Say what would you answer if asked in this manner? (Plato, Meno, 72a-b).

His interlocutor, here Meno, is expected to respond honestly and in the most intelligent way he knows.

I would say this, that they do not differ, in the manner that they are bees, one from another. (Plato, Meno, 72b).

In the case of Meno, the response is an indication of some kind of commonality that exists between the manifestations of virtue, which is to say that one example of virtue must compare with all others in quality or some other aspect. When the commonality becomes apparent, the interlocutors are able to say something about each of the examples:

If then I said after these things: tell me this very thing accordingly, Meno: in what thing do they not differ but quite all are the same. What do you say this thing is? Would you be able to tell me?
I would.
So it is truly the same case concerning the virtues: if they are many and varied, quite all of them have some one and the same form through which they are virtues, into which it is a fine thing for the one being asked by a questioner to have looked [in order to] demonstrate that thing which happens to be virtue. (Plato, Meno, 72b-c).

Recall the pattern-seeking that seems to be inherent in the literature of the ancient Greeks. Socrates is looking for patterns with his interlocutors. These patterns lead them to general statements about a given topic, like virtue, but the topic could just as well be matter, or time, or space. This pattern-seeking is a fundamental part of scientific inquiry, and the give and take resulting from Socrates' interactions with someone is the process of an interlocutor being relieved of his doxa, or opinion.[xviii] Socrates must first show that the opinion his interlocutor has is not true or perhaps in some way flawed. He usually accomplishes this task by demonstrating that should the young man accept his own view, he would inevitably fall into a contradiction or some other difficulty. When asked, Meno says that he believes all of the manifestations of virtue have some kind of commonality.

[Is] it...concerning virtue only, Meno, that there is one virtue of man, another of woman and of the others, or concerning health and size and strength is the case just the same? Does it seem to you that there is one health of man and another of woman? Or is there the same form in each case, if health is present whether in a man or in any other whatsoever?
Health seems to me to be the same both for a man and for a woman.
And what about size and strength? If a woman is strong, will strength exist with respect to the same form and the same strength? I am saying this as far as “the same”: strength does not differ in respect of being strength, whether in a man or in a woman. Or does it seem to you there is some difference?
It doesn't seem so to me. (Plato, Meno, 72d-e).

The idea here in Plato's Meno as elsewhere is that the doxa, or opinion, is reliant upon observations and belief alone, in other words becoming, which means that for Plato such a perspective is unstable. Naturally, the more stable thought comes from reasoning. Here reasoning is a development of observations and beliefs into a consistent, reliable argument that has a universal application. In other words, Socrates guides Meno through the topic of virtue by attempting to arrive at the eidos of virtue, or at least as close as possible to it. Remember that eidos is frequently translated as “form”, and the word itself derives from a verb that means “to see.” Eidos is linked to the mind through the sight organ, and mathematics is closer to eidoi. It is the most fixed way to make determinations as far as Plato is concerned; mathematics is an intermediary between the world of becoming and being (eidoi). Employing this method, Socrates guides his interlocutors into a way of thinking about the topic that is at once philosophical and open-ended. He and the given young man investigate through argumentation and continued refutation until they have come to an informed place of ignorance. They do not claim to know the topic, but they have a greater understanding of it because they admit their ignorance, especially because they have engaged in a dialogue about it. Such a state is sometimes called Socratic ignorance. The question that arises for us is how this process of question and answer relates to scientific endeavor when its topic is immaterial, science being decidedly about material objects and forces in the universe.

Ancient induction is reasoning from the particular to the universal. One begins with discernible instances of their topic and proceeds to examine them for common characteristics. Ancient deduction is reasoning from the universal to the particular. One begins with a universal claim about a topic and then applies it to given instances. The very structure of an inductive logical examination is inherent in the kind of conversation that Socrates has with his interlocutor. When the pair has found the similarity that makes specific examples the same, even though they are individually different, they seem to have found that which is common to them. This commonality Plato believed to be a deeper and more fundamental reality of a given thing. It has been discovered through reason and it is, for Plato, an immaterial part of each thing as it becomes. This thing that Socrates and his interlocutor have found is perhaps one eidos, which is the same fundamental aspect of material reality that underlies the monologue in Plato's Timaeus, but the examples are employed as the beginning of reasoning. Because the most fundamental and firm foundation is achieved through a connection with the mind, reasoning is sturdier than observation and comparison, for Plato at least. Deductive reasoning (in the ancient sense), therefore, is the most important of all activities of the mind for Plato, and deductive reasoning is fundamentally involved in the question and answer process in the dialogue. The examples employed give the interlocutors an arena in which deductive reasoning is able to reveal in some measure that absolute, the eidos, without which any one thing in the universe cannot become manifest. Remember that the eidos is accessible to the mind. It is deductive reasoning that reveals what a thing really is to the reasoner, its being. Thus, inductive and deductive reasoning are integral to the process, but deduction is the most significant.

One contribution of Plato to science that has lasted is the continued questioning and the finding of better answers in the context of examples leading through induction to deductive conclusions. Other thinkers before Plato had certainly reasoned. They had certainly used logic, but Plato puts the discussion on display. He demonstrates the reasoning that has eliminated certain opinions and arrived at much better insights through a rigorous process of induction and deduction. There is nothing more scientific than this kind of interplay. The structure of argumentation has not changed fundamentally, except that modern science seeks patterns in nature rather than an immaterial Platonic eidos, and modern logic is a different configuration of the same forms found in Plato's dialogues. The rules and structures have evolved, but inductive and deductive reasoning remain a fundamental part of scientific progress. So, a fundamental aspect of scientific reasoning is on display in the literary expression of Socrates' conversations with his interlocutors:

Is [justice] virtue, Meno, or some virtue?
What do you mean?
As with any other thing. For example, if you wish, I would say concerning roundness that it is some shape, but not simply that it is shape. I would speak of these things in this way because there are other shapes.
You speak rightly indeed, since I myself say that not only is justice a virtue but there are other virtues.
What are they? Do say, as I could mention other shapes to you if you urge me to do so. Tell me yourself then about the other virtues.
Courage seems to me to be a virtue, and moderation, wisdom, and magnanimity, and quite many others.
Again, Meno, we have experienced the same thing: we have again found many virtues while seeking one, albeit in another way. But one that is present through all of these we are not able to find.
I am not able to find as yet, Socrates, what you seek, one virtue for them all, just as in the other cases.
That is likely indeed , but I will be eager, if I have the ability, to lead us forward. For you understand that it is like this about everything. If someone should ask you what I mentioned just now: “What is shape, Meno?” If to him you said that it is roundness, if he said to you the very things I did, “Which of two is it? Is roundness shape or is it some shape?” You would doubtless have said that it is some shape.
I certainly would.
... So, too, if again about color he asked you the same thing what it is, and you said it is white, and after these things your questioner took up [again], “Is white color or a color?” you would have said that it is some color, because there happen to be other colors as well?
I would.
(Plato, Meno, 73e1-74c7).

A particular manifestation of a shape is no less a shape than any other and a particular color is no less a color than any other. The color-ness of color and the shape-ness of shape are the forms, or eidoi, of the subjects. Again, what Socrates and Meno want to comprehend is the absolute of each of these topics, which is attainable via deductive reasoning. Particular manifestations are not real; what the mind apprehends is. Additionally, Socrates has a slave determine the length of the side of a square. Part of the process is such investigation and re-investigation, but the actual reasoning of the geometric shape is deductive:

At first [the slave] did not know what the basic line of the eight-foot figure [square] was; just as not even yet does he know, but then he thought he knew it, and readily answered as if knowing, and he did not think himself lost, but now he does think himself at a loss, and even as he does not know, he does not think he knows.
You speak the truth.
So he is now better positioned with respect to the matter he does not know?
This seems to me to be.
Have we harmed him, having made him at a loss and numb like a the ray fish does?
It does not seem so to me.
Indeed, we have probably done something useful toward discovering how matters stand, for now, not knowing he would gladly seek to find out, but before he thought to speak well about the double figure [square] to many persons and repeatedly how there is need to have a [base] line double in length.
So it seems.
Do you think that before he would have tried to seek or understand that thing which he thought he knew while not knowing, before he fell into confusion and then believed he did not know and longed to know?
It does not seem so to me, Socrates.
Once numbed, has he benefited?
It seems so to me.

(Plato, Meno, 84a4-c9).

Socrates has the slave work out the area of a two-foot square:

Tell me, boy, do you know that a square figure is this sort of thing?
I do.
A square then is a figure having all these equal lines, being four?
Yes indeed.
And does it not also have these [lines] through the middle equal?
Yes.
And such a figure could be larger or smaller?
Yes indeed.
If then this side should be two feet, and this other side two feet, how many feet would the whole be? Consider it this way: if it were this direction two feet, and that direction only one foot, would the figure have been once [times] two feet?
Yes.
But when it is two feet that way, it comes to be twice two feet?
It comes to be [that].
… How many is twice two feet? Tell me once you have reasoned it.
Four, Socrates.

(Plato, Meno, 82b8-d4).

A two-foot side of a square produces an area of four feet. But then Socrates guides the slave into a difficulty. He makes the square four feet on each side:

Now another figure twice the size of this one could come about of this sort, having all equal sides just as this one does.
Yes.
How many feet will that be?
Eight.
Come on, try to tell me how long each side of that will be. The side of this one here is two feet. What is the side of that one which is its double?
It is clear, Socrates, that it will be double.

(Plato, Meno, 82d5-e2).

The slave does not know that once the size of the square has been doubled, the numbers used in the equation for determining the area of the square have changed. A square that has sides of two feet will have an area of four feet because the sides must be multiplied. The result is the same as if one added the numbers together, but when the sides have been increased to four feet, the product of four and four is the area, which is sixteen and not eight. The kind of reasoning involved in this equation is deductive. That is, deduction in the modern sense. If one knows the lengths of the sides of a square and calculates properly, then they will come to an inevitable conclusion.[xix] Double the length of one of the sides of a two-foot sided square makes an area of sixteen:

...do you say that a figure double in size comes to be from a line double in length? I am talking about this sort of thing: not long on one side and short on the other, but let it be equal in every part like this one, and double the size – eight feet. See if it still seems right to you that it will be based off of a line double the length.
It does.
Now the line becomes double its length if we add another of the same length from this quarter?
Yes indeed.
And the eight-foot square will be based on it, if four lines come to be of that length?
Yes.
Well, let us draw from it four equal lines. Is this here the other one which you say to be the eight-foot square?
Very much so.
And within this figure are four squares, each of which is equal to this one, the four-foot square?
Yes.
How much then does it come to be? Does it not come to be four times as much?
What else [would if be]?
Then is the square that is four times as much double?
No, by Zeus.
How many times as much is it?
Four times.
Then, my boy, not double but quadruple is the figure that has come to be based on a line twice the length?
You speak the truth.
And four times four is sixteen, no?
Yes.

(Plato, Meno, 82e12-83c3).

The conclusion is inevitable. Now, Socrates uses this example to prove another point. Like the geometric atoms, the argument here reveals something absolute about the answer, or so it seems. In other words, knowledge for Plato has a decidedly deductive aspect to it, which is linked to the certainty of the eidos and the form of a given thing. In this case, the form is that of a geometric figure. This certainty remains a part of the progress of scientific knowledge in the form of mathematics. Plato's Meno is especially important for our purposes not only because it is dialogue on display, but also because it demonstrates a fundamental part of Plato's notion of reality. The slave recalls eidoi that are part of his intellective activity. He does so while reasoning about a geometric shape, which is itself a mathematical figure, it being presentable in numbers. The calculation for a triangle can be thought, it can be written (A²+B²=C²). If the universe were to fall into disorder and all its objects were to combine into one homogeneous mass, the formula for a triangle would still be accurate, or so Plato thought. Plato takes the triangle's seeming permanence as a sign of its immaterial and undying quality revealed through deduction. We will see that mathematicians like Euclid employ a more pure form of deduction for their calculations,[xx] and these pure deductive calculations evolve into theoretical aspects of an hypothesis that is verified by tests. The effort at deduction in Plato has survived in modern science, but it has survived as a kind of theoretical certainty.

Furthermore, Plato's method of examination is a kind of ignorance that leads to knowledge, yet remains ignorance. This kind of investigation and re-investigation has spread to all the scientific disciplines in the form of articles and books on topics in specific fields that are influential, questioned and reexamined constantly. A worthy scientist will admit his ignorance and listen to others in his field and so the Socratic process is part of the progression of scientific knowledge. Socrates uses examples, like men having power and women being obedient, to examine what would be fixed, or stable, about each of the instances. The use of examples is the process of reasoning from the particular to the universal, which is basic inductive reasoning of the ancient kind and a seeking of repeatable patterns in nature. When one makes use of the examples in an argument, one reasons toward a universal, which is then used to construct an argument that is more fixed than the one arising from the examples. Once Socrates and his interlocutor have reasoned deductively, they have arrived at a better account than the examples. The examples are the becoming and the deductive reasoning is the effort at finding some aspect of that which is permanent: being.

An examination of Plato’s arguments is in order so as to understand how he develops his notion of material reality, but one must here be very careful. Plato reasoned as others do, but he understood that paradox is part of reasoning and he combined his reasoning with drama. We are examining only some of his arguments in his Timaeus and Meno. We are not claiming that our analysis of his argumentation is a universal part of his dialogue form. These are, as in the case of other thinkers, instances that come from particular works. Ordinarily, his argument would be not merely one interlocutor's assertions but two or more. In Timaeus Plato's reasoning is relatively straightforward. He gives the above account of the interactions of the geometric atoms, which can be taken as his theory of chemical interactions. His way of thinking can be broken down to a few relationships between categories of things found in the universe.

All elements that transform into other elements are elements that will pass into another shape.
No elements of earth are elements that will pass into another shape.
No elements of earth are elements that transform into other elements.

We have simplified Plato's reasoning in order to understand the essence of his argument, and one can see a certain consistency in his thoughts, but the premises are not necessarily true. There is a good deal of imaginative thinking in the assertion that minuscule bits of reality are shaped like icosahedrons, cubes, octahedrons, and tetrahedrons. This notion is merely conjecture, but if you follow and believe in Plato’s reasoning, the rest of his assertions follow.

All elements that will pass into another shape are elements that are interchangeable.
All elements called fire, air and water are elements that will pass into another shape.
All elements called fire, air and water are elements that are interchangeable.

If it is true that all elements that are interchangeable are elements that transform into one another and the above is true, then fire, air and water are elements that transform into one another. Like other ancient thinkers, Plato is making universal statements about aspects of material reality without qualification, other than his assertion that he is talking about a “likely” genesis of the universe.

All elements that are interchangeable are elements that transform into one another.
All elements called fire, air and water are elements that are interchangeable.
All elements called fire, air and water are elements that transform into one another.

Once we have accepted the argument that Plato makes about the size and shapes of the elements, how they combine and break one another down follows. All one must do is observe the geometric shapes that supposedly comprise the elements and learn into what they are likely to separate. If the ultimate piece of material reality is a triangle, then one wonders why an element is not further broken into the most fundamental shape, but one can also see the logic employed in Plato’s reasoning.

Plato's Meno offers another aspect of argumentation, one that is likened to his eidos. Plato argues in the form of geometry, which is mathematical in nature. The measurement of the square is specific and incontrovertible. When one establishes the units that measure the square, one has a kind of starting place, or reference point. The measurement is a certainty that will allow Plato to make a clear and absolute assertion about the area of the square. The two foot square:

The area of a square with sides of two meters each is four, because the product of two and two is four. There is no escaping that conclusion. It is not an imagined belief, nor is it a set of particulars that supposedly lead to a universal conclusion. The measurement of the square's area will always be four meters. When the slave makes a mistake and doubles the side of four meter's length, he demonstrates that he does not understand what is the calculation. When he reexamines the four meter square and realizes that he must take the product of the side and the other side, he understands the inevitable conclusion: the area of a four meter square is sixteen meters, not eight.

The four foot square:

The lower corner is representative of how all of the squares are sectioned, so each square that comprises the larger square possesses four squares, resulting in sixteen squares. This is deductive reasoning in the form of mathematical measurement. One must come to the conclusion, given what information is available; it is inevitable. The absolute nature of the inevitable conclusion is the kind of conclusion Plato seeks in all his reasoning, which is why he is attracted to the idea of an eidos and mathematics. A similar kind of deductive reasoning is the theoretical and mathematical reasoning that remains in modern science. Enclosed in its own system, a calculation is not incorrect as long as it follows the rules of logic or mathematics, but its application may be incorrect. In other words, an equation may not fit what moderns call objective reality, and so when tested an equation may have its own consistency, but not apply to actual things. When Socrates and Meno seek virtue in its most elemental and essential form, they seek the certainty of a universal virtue. Here Plato applies mathematical methods to the search for an absolute moral. Yet, this kind of certain system may be applied to any subject, and such application is what remains of his method in scientific progress and reexamination. Science is, in part, a dialogue.

[i] Plato may not have been responsible for as much science as once thought to be the case. For an argument against his being the one who presented a scientific method employed in scientific circles, see Zhmud. Plato may also not have been responsible for the principle of “saving the appearances”, fundamental to Greek geometry (See Lloyd), and customarily attributed to him. Still, Pirmin Weithofer asserts that for Plato abstract or mathematical structure is necessary for pure knowledge, both of which are necessary elements of science. There is no shortage of debate.
[ii] Interest in Timaeus during the twentieth century has declined and resurged. It is presently taken seriously as philosophy, if not physics. Some see Plato's Timaeus as metaphorical, or mythic, while others see it as more literal. For the mythical interpretation, see A.E. Taylor. For the more literal, see Cornford. This text treats Timeaus as mythical with literal elements. Most of the contentions are taken literally. Donald Zeyl treats the history of commentary on Timaeus.
[iii] Charles Kahn reads Timaeus as “a constructive account of phenomenon within the field of perception and change”, which means that expectations for accuracy as to what comprises the universe ought to be low. Plato must contend with opinion and becoming – not to mention matter – and thus his account will necessarily be unstable. For more, see Kahn, Cornford, Taylor.
[iv] For Francis Cornford Plato's sense-perception is “unreasoning” and does not grant full understanding. He quotes Proclus when he states that sense tells us apples are a specific color and shape, but reason tells us they are apples. Sense-perception will also never alert us to the fact that the sun is not a small ball in the sky, but reason will. Reason coupled with sense-perception comprise our good judgments. For more on the relationship between reason and perception, see Cornford.
[v] Dialectic (dialogue in Plato's works) is more precise and fundamental than even mathematics. Timaeus is not dialogic and so its exposition exists on a more superficial plane.
[vi] For more on the relationship between being and becoming and its debate, see Cornford, Kahn, Johansen.
[vii] T.J. Haarhoff points out that the modern conception of atoms is closer to Plato's conception of atoms than Democritus' conception. The regular solids depict atoms as regular mathematical entities; modern math and science do the same thing. For more, see Haarhoff, Cornford, Pohle, Cleary.
[viii] For an account of flux in Timaeus, see Mohr. For a thorough account of the elements as causes, see Broadie. For an account of the harmony, or commensurablility, of the elements and their “chemical” interactions, see Brisson and Meyerstein who believe that Plato proves systematic verification was not rejected because the chemical theory of the elements works in common interactions.
[ix] http://www.mathpages.com/home/kmath096/kmath096.htm.
[x] For a brief but sophisticated view of the forms in Timaeus, see Ostenfeld. For an explanation of why the theory of forms is a part of Timaeus, see Ferber and also Kahn (1985).
[xi] Some scholars see the demiurge as metaphorical; some see it as literal. For the metaphorical view, see Cornford.
[xii] For a good, basic explanation of the relationship between forms and modern physics, see Joad.
[xiii] The role of number in Platonic Forms is somewhat ambiguous. While they play an intermediate role between being and becoming in Plato's Republic, some scholars believe that number is a fundamental part of the theory of Forms: the one, unlimited and limit – called the indefinite dyad – generates the Forms.
[xiv] These circles are the celestial spheres on which heavenly bodies rotate.
[xv] If there is a need to explain material becoming in spite of the geometric atoms, then the atoms themselves cannot be becoming. They must be being or the intermediate kind of being-becoming. Such a need means that the geometric atoms are akin to eidoi. For more on their geometric composition, see Johansen, Cornford, Kahn.
[xvi] Images reside in the world of becoming for Plato. The world of being actually is, and what receives the Forms as an image is the receptacle. Some see the receptacle as potential, like Aristotle's prime matter; some (Kahn) see it as three-dimensional space. It is likened to a base for perfume and clay as well as water reflecting an image. For more on this issue, see Cornford, Kahn, Sedly, Johansen, especially Miller.
[xvii] One must differentiate between mere questioning and Plato's dialectic; these are not the same things. Dialectic, sometimes called dialogic, is a qualitative seeking and a process that does not believe its practitioners know, while mee questioning may come from scholars who through modern mathematics or logic do believe they know.
[xviii] It is important to note that Plato sought the most absolute answers to philosophical questions. Modern science has given up on the formation of universal answers in the form of absolute resolutions. Science now thinks in terms of probabilities, whereas ancient philosophy sought absolute, universal answers. Thus, Plato sought something fundamentally different from what science now seeks. The difference is one of the possible differences between philosophy and science.
[xix] Not surprisingly, modern mathematics questions even the certainty of deductive reasoning, but that is another – most interesting – issue.
[xx] Plato thought that there was a more refined method than mathematics: dialectic (See Mueller). For more on how closely Plato's proof in Meno resembles Euclid's axiomatic method, see Haarhoff, Szabo, Kahn, Wolfsdorf,

PLATO BIBLIOGRAPHY

Bianchi, Emanuela. 2006. “Receptacle/Chōra: Figuring the Errant Feminine in Plato's Timaeus.” Hypatia 21, No. 4: 124-146.
Brenton, Lawrence. 2013. “Plato, Poincare, and the Enchanted Dodecahedron: Is the Universe Shaped Like the Poincare Homology Sphere?” Math Horizons 20, No. 3: 12-17.
Brisson, Luc and Meyestein, Walter F. 1995. Inventing the Universe. Albany.
Broadie, Sarah. 2012. Nature and Divinity in Plato's Timaeus. Cambridge, New York.
Cleary, John J. 1997. “Plato's Teleological Atomism,” in Interpreting the Timaeus-Critias. Calvo, Thomas and Brisson Luc eds. Germany.
Cornford, Francis MacDonald. 1956. Plato's Cosmology. London.
Eves, Howard. 1969. “A Geometry Capsule Concerning the Five Platonis Solids.” The Mathematics Teacher 62, No. 1: 42-44.
Ferber, Rafael. 1997. “Why did Plato maintain the 'Theory of Ideas' in the Timaeus?,” in Interpreting the Timaeus-Critias. Calvo, Thomas and Brisson Luc eds. Germany.
Finkelberg, Aryeh. 1996. “Plato's Method in Timaeus.” The American Journal of Philology 117, No. 3: 391-409.
Gill, Mary Louise. 1987. “Matter and Flux in Plato's "Timaeus".” Phronesis 32, No. 1: 34-53.
Glenn, S. 2011. “Proportion and Mathematics in Plato's Timaeus.” Hermathena, No. 190: 11-27.
Grabiner, Judith V. 1988. “The Centrality of Mathematics in the History of Western Thought.” Mathematics Magazine 61, No. 4: 220-230.
Gulley, Norman. 1960. “The Interpretation of Plato, Timaeus 49 D-E.” The American Journal of Philology 81, No. 1: 53-64.
Hackforth, R. 1944. “Notes on Some Passages of Plato's Timaeus.” The Classical Quarterly 38, No. 1/ 2: 33-40.
Haarhoff, T.J. 1962. “The Return of Ancient Science,” Greece & Rome 9, No. 2: 128-133.
Joad, C.E.M. 1933. “Plato's Theory of Forms and Modern Physics.” Philosophy 8, No. 30: 142- 154.
Johansen, Thomas Kjeller. 2004. Plato's Natural Philosophy. Cambridge.
Kahn, Charles. 1985. “The Place of the Statesman in Plato's later Work,” in Reading the Statesman, Proceedings of the III Symposium Platonicum, ed. Ch. J. Rowe. St. Augustin.
____________. 2013. Plato and the Post-Socratic Dialogue. Cambridge.
Kotre, Ronald F. 1981. “THE DODECAHEDRON IN PLATO'S "TIMAEUS".” Reheinisches Museum für Philologie, Neue Folge 124, 3/ 4: 212-222.
Lee, Edward N. 1967. “On Plato's Timaeus, 49D4-E7.” The American Journal of Philology 88, No. 1: 1-28.
____________. 1966. “ON THE METAPHYSICS OF THE IMAGE IN PLATO'S "TIMAEUS".” The Monist 50, No. 3: 341-368.
Lloyd, G.E.R. 1978. “Saving the Appearances,” Classical Quarterly 28: 202-222.
Miller, Dana. 2003. The Third Kind in Plato's Timaeus. Germany.
Miller, Harold W. 1957. “The Flux of the Body in Plato's Timaeus.” Transactions and Proceedings of the American Philological Association 88: 103-113.
Mills, K.W. 1968. “Some Aspects of Plato's Theory of Forms: "Timaeus" 49c ff.” Phronesis 13, No. 2: 145-170.
Mohr, Richard. 1980. “The Mechanism of Flux in Plato's Timaeus,” Apeiron: A Journal for Ancient Philosophy and Science 14, No. 2: 96-114.
___________. 1980. “Image, Flux, and Space in Plato's "Timaeus".” Phoenix 34, No. 2: 138- 152.
Mortley, Raoul J. 1967. “Primary Particles and Secondary Qualities in Plato's Timaeus.” Apeiron: A Journal for Ancient Philosophy and Science 2, No. 1: 15-17.
Morrow, Glenn R. 1950. “Necessity and Persuasion in Plato's Timaeus.” The Philosophical Review 59, No. 2: 147-163.
Mueller, Ian. 1969. “Euclid's Elements and the Axiomatic Method,” The British Journal for the Philosophy of Science 20, No. 4: 289-309.
__________. 1989. “Joan Kung's Reading of Plato's "Timaeus".” Apeiron: A Journal for Ancient Philosophy and Science 22, No. 4: 1-27.
Nikulin, Dmitri. 2000. “A NEW INTERPRETATION OF PLATO'S COSMOLOGY: "TIMAEUS" 36 B-D.” Methexis 13: 113-118.
Ostenfeld, Erik. 1997. “The Role and Status of the Form in the Timaeus: Paradigmatism Revised?,” in Interpreting the Timaeus-Critias. Calvo, Thomas and Brisson Luc eds. Germany.
Paquette, Leo A. 1982. “Dodecahedrane--The Chemical Transliteration of Plato's Universe (A Review).” Proceedings of the National Academy of Sciences of the United States of America 79, No. 14: 4495-4500.
Phillips, J.P. 1965. “The history of the dodecahedron.” The Mathematics Teacher 58, No. 3: 248- 250.
Pohle, Naomi. 1971. “The Mathematical Foundations of Plato's Atomic Physics,” Isis 62, No. 1: 36-46.
Reshotko, Naomi. 1997. “A Bastard Kind of Reasoning: The Argument from the Sciences and the Introduction of the Receptacle in Plato's "Timaeus".” History of Philosophy Quarterly 14, No. 1: 121-137.
Robinson, T.M. 1993. “The World as Art-Object: Science and the Real in Plato's "Timaeus".” Illinois Classical Studies 18: 99-111.
Sedly, D. 1982. “Two Conceptions of Vacuum,” Phronesis 27: 175-192.
Shorey, Paul. 1889. “The Timaeus of Plato.” The American Journal of Philology 10, No. 1: 45- 78.
Steel, Carlos. 2003. “Why Should We Prefer Plato's 'Timaeius' to Aristotle's Physics" Proclus' Critique of Aristotle's Causal Explanation of the Physical World," Bulletin of the Institute of Classical Studies Supplement, No. 78: 175-187.
Szabo, A. 1960. Anfänge des euklidischen Axiomenszstems. Archive for History of Exact Sciences 1, no. 1, 37-106.
Taylor, A.E. 1928. A Commentary on Plato's Timaeus. Oxford.
Unguru, Sabetai. 1975. “On the Need to Rewrite the History of Greek Mathematics.” Archive for History of Exact Sciences 15, No. 1: 67-114.
Verdenius, W.J. 1982. “Plato, "Timaeus" 53 A 7.” Mnemosyne, Fourth Series 35, Fasc. 3/ 4: 333.
Vlastos, Gregory. “Elenchus and Mathematics: A Turning-Point in Plato's Philosophical Development”, The American Journal of Philology 109, No. 3: 362-396.
Weithofer, Pirmin Stekeler. 1992. “Plato and the Method of Science,” History of Philosophy Quarterly 9, No. 4: 359-378.
Wolfsdorf, David. 2008. “The Method ejx uJpoqevsewV at Meno 86e1-87d8,” Phronesis 53, No. 1: 35-64.
Zhmud, Leonid. 1998. “Plato as 'Architect of Science',” Phronesis 43, No. 3: 211-244.
Zeyl, Donald J. 1975. “Plato and Talk of a World in Flux: Timaeus 49a6-50b5.” Harvard Studies in Classical Philology 79: 125-148.
____________. 2000. Plato “Timaeus” Indianapolis, Cambridge.