Introduction
Science cannot be defined in only one way; it is a kind of inquiry that never finds complete description. Thinking and verifying one's thought have always been a part of the human experience; we have always observed, found patterns, argued and systematized, but science puts these things into a specific order and demands a certain kind of verification for its assertions. It is thus a natural ability to order that comprises science, and it is not foreign to any people, though it emerges gradually over long periods. Saying that there was no science here or there – then or later – is misleading, but because neither our particular ordering, nor method, was present in the ancient world, we must say that science did not exist in antiquity. Still, it existed in pieces. The root of the word is scio, a Latin verb meaning “to know.” Modern science is an attempt at knowledge of a given subject through reason and verification, relying on probabilities. It attempts to reason about the likelihood of a given event or process. In knowing the probabilities of things, science allows humans to control their environment and manipulate specific processes in that endeavor. Science has many geneses: political, social, economic, geographic, ethnographic and intellectual, but as Bernard Pullman points out science cannot flourish without free expression, a willingness to consider different theories, openness toward debate and tolerance from public authorities.[i] It is a body of theoretical knowledge that employs technology in the solution of problems and the current belief about the nature of reality. It is a rigorous and precise attempt to attain and understand an assumed objective reality, and as such it filters out speculation, conjecture and imagined beliefs in favor of empirical verification of hypotheses. Its reach extends to almost every human endeavor: physics, medicine, politics, economics et alia. Science has made the human family master of nearly all of the earth and because it did not exist in its complete form in antiquity, it is necessary to provide a tentative definition, one that will allow us to see in some measure and how ancient inquiry survives in contemporary scientific analysis. This text focuses specifically on physics, and so our definition must center around physical change, a central unifying principle and a system that explains how that principle functions in the universe.
Science is a manner of understanding the behavior of nature, using deductive reasoning in the form of logic or mathematics to establish hypotheses. It empirically verifies these hypotheses through a process of experimentation, which involves understanding the interactions of things in material reality – other belief systems notwithstanding. Here is a tentative, general definition of science that is useful for understanding the continuity between ancient and modern methods for understanding. G.E.R. Lloyd claimed [ii] that science is “certain investigations that are continuous with what is normally included in our term science [which were] initiated in ancient Greece”, yet while valuable and accurate, Lloyd’s perspective leads to R.K. French’s suggestion [iii] that “to see science in antiquity we need to have a definition of science so broad as to be meaningless.” Our tentative definition is needed in order to begin discussion and to refrain from meaninglessness. It is not complete, but it allows a discussion about what may be called "ancient science.”
On the one hand, science is an intellectual inquiry into a particular subject-matter and on the other, it is the empirical or experiential verification of that continued inquiry. One part cannot be science without the other. Physics comes to mind when one uses the word “science”, perhaps because we have inherited Aristotle’s prejudice that knowledge of physics is knowledge of everything.[iv] Our aim is to discuss science on a fundamental level, so a discussion focusing on the thought process of science will reveal some measure of how ancient inquiry was a continuous investigation without the definition being meaningless. The thinking in science and its manner of verification in its most fundamental form are then our topics, and in order to understand the epistemology of science, we must understand some significant part of logic. Along the way, we will be able to discuss some of the empirical dimensions of ancient investigation.
Deduction and Induction
Logic is the engine of reason and science is only as strong as its reasoning. Reasoning involves the drawing of inferences. The connections that exist between accepted facts or postulates provide a new assertion. These new assertions proceed from what one does know to what one did not know: inferences. One calls such connections logic and the stronger the connection the more potent the reasoning; the more potent the reasoning, the truer the inference. There are two significant kinds of logic that are part of a rigorous system of thought used to investigate nature. These are deduction and induction.[v] The ancients understood these terms differently than we do, naturally, and it is valuable to point out the general differences between the ancient and the modern conceptions of logic in order to bring into sharper relief how ancient thought founds modern science. In the ancient view, deduction is a thought process that proceeds from universals to particulars. One begins with a universal conceptual thought, perhaps an abstraction, and proceeds to comprehend a subject on the basis of characteristics that define the whole of a category. What is consistent, what is cohesive and what follows thus from generalities are primary concerns of the ancient notion of deduction. Ancient induction proceeds from the particular to the universal. One begins with an observation or a sense that some members of a category possess specific characteristics and then one proceeds to understand universals through perhaps comparison. A syllogism is a set of assertions about the world that together allow for a “bearing in” or inference from statements that are accepted as true to a previously unrealized assertion.
Example one:
All cats are quadrupeds. Assertion
All lions are cats. Assertion
Therefore, all lions are quadrupeds. Inference
If the connections are strong and real, the inference is said to be true. If the connection is faulty or non-existent, then it is said to be false. Because it is true that all cats are quadrupeds and all lions are cats, it is true that all lions are quadrupeds. Here is a possible connection between thoughts, entities, or happenstances that possesses an internal consistency. It speaks of universals in the sense that it expresses the whole of a category of things. All members of the set of lions are quadrupeds if they fit into the class of cats, which in turn is a subset of quadrupeds. There is inherent in this simple syllogism a mathematical dimension in the sense that it makes an assertion about sets of things. Ancients did make distinctions between what they perceived as universals in particular manifestations of things – what we may call abstraction – and the particular things themselves. The particular things exist in the realm of becoming; they come into being and proceed to grow to fruition and decrease, then perish. They have no permanence in the sense that they change. In seeking fixed and absolute aspects of reality, ancients generally sought permanent categories of things perceived in the world. The expression of a connection between particulars is a different form of assertion.
Some humans are owners of sports cars. Assertion
Some owners of sports cars are safe drivers. Assertion
There is no conclusion here because the connection made between particular statements is not strong enough to generate a strong inference (more below). These assertions talk of only a portion of a class of things: at least one member of a category. In the first sentence at least one member of the class of humans is a member of the class of safe drivers, and the same with owners of sports cars and safe drivers in the second sentence. So, when making assertions of this kind, one makes statements about only parts of whole categories of things. In particular and universal statements such as these, there are subject terms and predicate terms, indicated by the “S” and the “P” in the examples below.
All S are P.
Some S are P.
These are the subject and the predicate of the given statement. There are also middle terms, indicated by the “M” in the examples below.
All M are S.
Some P are M.
The middle term is the category that is common to both the other terms when a logical connection can be made. So, in example one “cats” is the middle term. It has something in common with both “lions” and “quadrupeds.” This commonality is what allows one to draw an inference. Two statements of categories together coupled with a conclusion comprise a syllogism. A syllogism draws an inference when it makes a connection, and that connection thus allows a conclusion. “All lions are quadrupeds” is the inference made through the connection and thus it is the conclusion. In Aristotelian, syllogistic logic there are four types of assertions whose elements possibly have a connection. An “A” statement asserts that one whole subject set is a subset of the predicate set:
- All S are P.
- An “E” statement asserts that one whole subject set is excluded from a predicate set (and vice versa).
- No S are P.
- An “I” statement asserts that one part (at least one) of a subject set is a subset of the predicate set.
- Some S are P.
- An “O” statement asserts that one part (at least one) of a subject set is excluded from the predicate set.
- Some S are not P.
The first two sentences are universal; they assert something about all of at least one set of things. The third and fourth sentences are particular; they assert something about at least one of a set of things. The majority of ancient thinkers looked for first principles or fundamental first elements that would allow them to explain change and continuity in processes encountered in physical happenstances. They believed they needed to find a permanent aspect of reality that was the foundation for impermanence. They thus sought what was fixed and lasting and attempted to base their arguments on permanence even as some ancient thinkers embraced change as a fixed element. In other words, they sought universals. A and E statements were the kinds of assertions, then, that they wished to employ in their reasoning.
Induction as understood by ancients operates from the other direction. One proceeds to make the same kinds of connections, but from particulars to universals. I and O statements are inductive statements, asserting something about at least one member of a set of things and asserting something about particular manifestations (this specific cat). The connections made between parts of sets by their nature cannot be as reliable as those made about all of the members of a certain set. An assertion about all of one set and all of another set encompasses all possibilities, and so is obviously a much more reliable connection. Again, the above example.
All cats are quadrupeds.
All lions are cats.
Therefore, all lions are quadrupeds.
There is certainty in the statement “All lions are quadrupeds” because the sentences above it assert something about all of a given category. If we alter these statements and make them particular, they have a very different meaning.
Some cats are quadrupeds.
Some lions are cats.
There is no universal, and therefore reliable, connection between these statements because they make assertions about only some of a given category; we do not even know how many of a given category possess the characteristics asserted. If some cats are quadrupeds and some lions are cats, then the lions that are quadrupeds may not be the same cats; all of them may be or only some. We have no way of drawing a firm inference about the “some” in either sentence. Ancient thinkers generally sought the certainty that comes from the strong connection of a universal. In fact, many ancients perceived particulars as unreliable because they thought of them as unstable. One can see how dissatisfying it would have been for ancient thinkers to discover rules about logical connections only to find that logic cannot find the very universals it was meant to discover. Centuries of investigation passed before scientists disposed of the attempt to find universals in favor of probabilities.
Deduction and Induction in Modern Science
The modern view of logic and its limitations is different. When an argument has a good form and the connections it makes seem real and verifiable in terms of their relation to one another, we call the argument valid. So, that we have made a firm connection between lions and quadrupeds in the above example is that argument's validity. There is a conceptual connection between the different categories. When, however, an argument possesses not merely good form and connection but also has as its premises verifiable, true elements of the world (like facts or accepted conditions of existence), then one calls it sound. So, that lions who are cats exist in the world and that cats are actually quadrupeds along with the connections between them makes the argument sound. As one may imagine, an argument can be valid and unsound. But an argument cannot be sound and not valid because the connections as well as true statements need to exist for an argument to be sound. So, the following argument is valid.
All paper towels are men with socks.
All unicorns are paper towels.
Thus, all unicorns are men with socks.
The statements do not need to be true, but the connections between the stated categories need to exist. If the form of the argument is good and if the connection is present, then the argument is valid. Additionally, one must accept the conclusion. If it has good form it is valid, even if it is nonsensical. Our initial example argument is sound.
All cats are quadrupeds.
All lions are cats.
Therefore, all lions are quadrupeds.
There are such things as cats in the world and cats are actually quadrupeds. Also, there are such things as lions and lions are actually cats. Because the categories make a strong connection, the argument is valid; because the statements are true and because the argument is valid, the argument is sound.
Deduction in the modern sense means that if we accept the premises of the argument, then the conclusion will not only naturally follow, but we must accept the conclusion. The certainty of a very strong connection is deductive, given its assumptions. Mathematics is a good example of deductive reasoning. It presents clear and certain conclusions from commonly accepted constants, or the most certain calculations possible. Modern deductive reasoning is not necessarily in harmony with its subject. In other words, the internal consistency of a deductive argument may compel someone to accept the conclusion, but the assertions used in the argument may have little to do with reality. If one creates a perfectly cohesive mathematical thesis, it may be valid, but have little to do with how things interact in material reality. Scientists verify their arguments through an empirical means, which is, of course, the experiment.
Induction for moderns is the discovery of connections, but they are considerably weaker than those made by deduction, and modern induction is not concerned with particulars in the same way that ancient induction concerns itself with particulars. A modern inductive argument asserts something about the probability of some conclusion to be true. Obviously, there are different degrees of probability. So, an inductive argument in the modern sense is one that will make a kind of prediction about an event. Given the facts that we possess about the earth and its relation to the sun we can predict with a great amount of certainty that the sun will rise in the east and set in the west tomorrow. So, it is an argument that asserts a specific occurrence will take place with a great deal of probability, given certain circumstances, but not that the occurrence must take place. There is a predictability to the argument, but not absolute certainty. Thus, the probability. One sees this kind of argument when one reads the prediction for the weather. There is a certain percentage chance that rain will fall, for instance. The percentage is the probability of rain, induced by the circumstances that are taking place at a given time. So, if there are dark clouds in the sky and one hears thunder, one can make a relatively certain induction that rain will fall. Inductive arguments guide modern scientific investigation because the scientific search for universals has ended, or it has at least paused. We will return to the particulars of logic and Aristotelian logic rules later, but now it is necessary that we understand what part of this manner of thinking we are investigating. Other kinds of logic exist besides the syllogism. Propositional logic is similar to syllogistic logic, but it is a form of logic in which the fundamental components are whole statements or assertions. Propositional logic is the combining of two or more sentences, or propositions, in order to find more complicated assertions of truth. Propositional logic, then, operates in the same manner as syllogistic logic, but with more assertions. In fact, all logic operates on the same level in one sense. All of logic attempts to make connections based on the truth and falsity of certain statements, the categories that they represent and the connections or relationship between them. Symbolic logic is a development of propositional logic, but with different sigla. It replaces purely linguistic statements with symbolic ones and is comprised of a given set of proven connections that lead to more complex connections. Predicate logic makes use of the same symbols as symbolic logic, but accounts for the complete sets and partial sets that one sees in syllogistic logic. Mathematics is only a short step away from these kinds of logic in that it is in part a quantification of similar assertions. We will cover only a few of these kinds of logic, but we want to keep in mind that logic is not monolithic. There is a great similarity between kinds of logic, but they have different forms. The most fundamental aspect of logic is, again, that it makes connections, or in some cases disconnections, between things. Every kind of logic performs that function.
Induction as a Part of Scientific Method
We are examining the engine of science, its logical apparatus, in order to learn about ancient contributions made to the current scientific method. We are interested in the history of science, but merely stating at what conclusion a particular thinker arrived is hardly satisfying when we want to comprehend science as a way of determining truth and a way of discovering “laws” of the natural world. The awareness and manipulation of natural processes have allowed humans to possess great control over their environment and given us the modern age, as well as the virtual age. Humans have even journeyed outside the planet because of the thought that drives science. We want to keep the distinction between deduction and induction in mind as we examine systems of thought that have contributed to an overall scientific method employed today. We will come to some understanding of how much and in what way each element of thinking survives in current scientific method.
How, then, precisely does the thought of science operate and how does it demonstrate what it asserts is actually true about the world are fundamental questions for us. One part of science looks for the causes of things, so we need to have some way of understanding causes.[vi] There are three definitions of cause that apply for us. There are necessary conditions, sufficient conditions and sufficient and necessary conditions. Necessary conditions are conditions needed for something to happen, but in some cases in themselves are not enough to make something occur. Water is necessary to produce life, but it is hardly sufficient. If it were, we would have been able to create new forms of life at will, even in the ancient world. Water is a necessary cause for life. A sufficient condition is a condition, or cause, that itself is enough to make something happen. The chopping off of someone's head is a sufficient cause of death, but other methods prove efficacious. Shooting, stabbing or strangling a person will result in their death if done in a specific way. A necessary and sufficient condition is a condition that will in itself produce the desired effect, and nothing more than it is necessary. The acceleration of a body is caused by the action of some force upon it.[vii] Nothing more or less is needed for acceleration to come about.
If X is a sufficient condition for Y, then if X occurs then Y occurs. Beheading is our example. If someone beheads another person, that person will die. Additionally, if X is a necessary condition for Y, then if Y occurs X occurs, but not necessarily the other way around. So, if I am driving my car, my car's engine must be running, but simply because my car's engine is running does not mean that I am driving my car. Similarly, the absence of X is a sufficient condition for the absence of Y, if and only if Y is a sufficient condition for X. So, if there is no acceleration of my car, then there must be no force, its engine, acting upon it.
In a similar fashion, the absence of X is a necessary condition for the absence of Y if and only if Y is a necessary condition for X. If my car's engine is not running, then it must be that it has not been started, because starting a car is needed for its engine to be running. Lastly, X is not a sufficient condition for Y if X occurs without Y. If it so happens that I started my car and it is not moving, then starting my car is not a sufficient condition for it to move. And, X is not a necessary condition for Y if Y occurs without X. It is necessary, but not sufficient. If I started my car without wearing my hat, then wearing my hat is not needed for starting my car.
We talk about these conditions because they will be necessary for understanding how the reasoning process works in evaluating causes of things. Remember that for our purposes there are two realms in which science works. The one is more theoretical, and it involves making abstract arguments about things in the world. We use statements, propositions, axioms, mathematics and the like to make these arguments. They may apply to material reality and they may not. The other is more empirical, and it involves verifying those valid but perhaps not sound arguments upon circumstances in the world. When we experiment upon something, we find out if our seemingly logical standpoint really speaks to some objective truth about how things operate. So, now we need to understand what methods there are for verifying our reasoning. We will cover five methods for demonstrating causal connections.[viii] These are basic ways our reasoning may be involved in making scientific inferences.
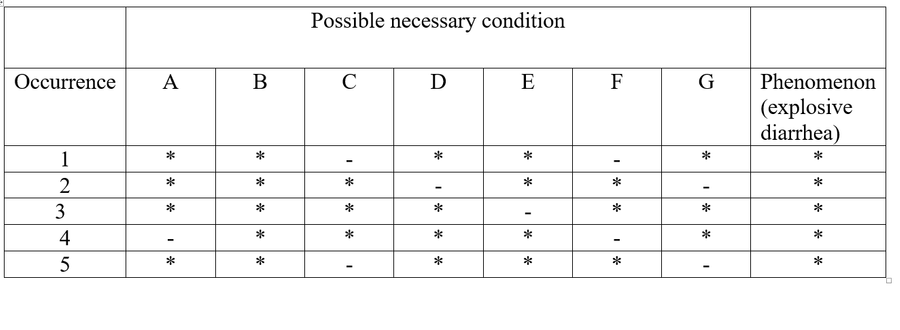
The Direct Method of Agreement demonstrates the relationship between an effect and a necessary condition. One looks for a single element that is present in many occurrences where the effect sought is also present. The one element that is present when the effect is present is thought to be the cause. An example:
Seven individuals came down with explosive diarrhea while eating in the
same restaurant. They all ate different food, but used Momma's Sweet
Red-Hot sauce. The hot sauce was the only commonality.
Food scientists concluded that the ailment came about because of the hot sauce.
The following table shows how the conclusion came about. The occurrences are the individuals who ate at the same restaurant. The possible necessary conditions indicate the possible foods eaten. An asterisk shows the presence of something and the dash absence. The condition that is present in all of the occurrences is the condition taken to be the cause of the malady.[ix]
Because the hot sauce (B) is the only common condition in all occurrences, it is taken to be the necessary cause. The idea is to eliminate as many of the necessary conditions as the information permits. When only one condition remains, one has the possible cause. Note that this argument is inductive. It uses evidence to examine what may be present when the effect is present in order to determine a connection and that connection is probable to some degree. Some other cause may have been overlooked; the malady may have been transmitted through a combination of things. It may have been possible that some other condiment caused the malady. In other words, the argument does not state that all those not using the hot sauce did not fall ill. Here is what it says: X is not a necessary condition for Y if X is absent when Y is present.
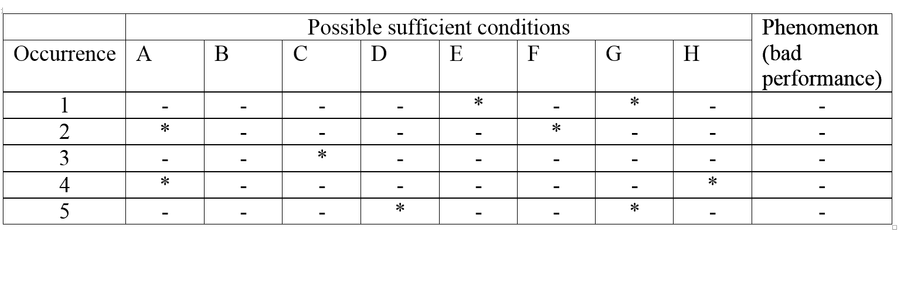
The Inverse Method of Agreement demonstrates the difference between an effect and a sufficient condition. The idea is roughly the same, but one tries to identify an element that is absent from a number of occurrences in which the effect is also absent. The absent element is taken to be the cause. An example:
Five students performed worse on exams at Sultan University. A list of several present and absent factors were examined as possible causes. Among eight likely causes, only one was absent for all five students: their cell phone.
The argument asserts that the absence of a cell phone contributed to the diminished performance of the students. Here is a representation of the argument:
The idea is similar to the Direct Method of Agreement, except we look for an element that is absent. B represents their cell phones. Among all the other possible causes the only one that is absent when good performances are absent is a cell phone. One attempts to eliminate as many possible causes as one can. The rule used here is one for sufficient conditions: X is not a sufficient condition for Y if X is present when Y is absent. This argument is inductive as well, since not all of the important conditions have been determined. Also, two or more elements can be acting in conjunction in order to cause the phenomenon. One can only say that we have narrowed the possible causes and that the one absent possible cause may be the actual cause. The argument also pertains only to the persons who have participated, not to all possible students. Students in general may act in a very different way. One can see the probability involved in this argument. It is informative, but one can obtain only a degree of certainty because one does not possess all possible information. If more occurrences are added, more possible causes may be considered. Additional conditions may significantly impact the conclusions. Giving cell phones to students may improve their performance, but that is not the only element that may improve performance. Perhaps more rigorous study or less consumption of alcohol may improve performance as well.
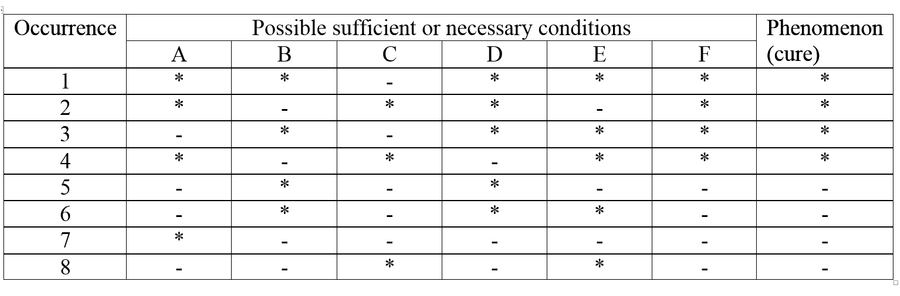
The Double Method of Agreement is the combination of the direct method of agreement and the inverse method of agreement. This method identifies necessary and sufficient conditions. This method is often used by researchers to determine the effectiveness of drugs on humans or animals. An example:
- Eight members of the Men's Club of America contracted a rare form of plague.
- Hearing about it, a doctor flew to their clubhouse with a serum that was thought
- to be a cure. When the doctor arrived, only four of the men would accept the
- serum, but all eight had previously treated themselves with various club remedies.
- After a short time the four who received the serum recovered while the other
- four did not. Among those who recovered, no single club remedy had been
- given to all; and among those who did not recover, every club remedy had
- been given to at least one. The doctor concluded that the serum was a
- cure for the disease.[x]
Here is a table representing the Double Method of Agreement:
This method measures the sufficient and necessary causes, as one can see from the four asterisks on top and the four dashes on the bottom. The asterisks represent the occurrence of the cure and the dashes represent the absence of the cure. F is the element that is present when the cure is present and absent when the cure is absent. The first four asterisks eliminate A, B, C, D, and E as necessary conditions because they are absent when the cure is present. The last four dashes eliminate A, B, C, D, and E as sufficient causes because they are present when the cure is absent. The argument is still probable, because there may be things overlooked, but there seems to be a reasonable degree of probability that the cure is F because it is the only factor that is present when the cure is present and absent when the cure is absent. A combination of things with F may be a possible cure, but because we have argued for necessary and sufficient causes the likelihood that a combination of things with F cured the patients is significantly diminished.
The Method of Difference finds one single, present element in an occurrence that is absent in another, similar occurrence where the phenomenon is absent. This element is how the two occurrences differ and it is supposed that this element is the cause. Sometimes called the laboratory method, the Method of Difference is used by researchers in very controlled conditions. This method is obviously one that interests us a great deal. One can see parts of the other methods in it, and it is what many scientists use in order to verify arguments. Their arguments, or their hypotheses, may have good connections, and so they may be valid, but the verification testifies that the argument applies to a given situation. An example:
- Two identical white mice in a controlled experiment were given identical amounts
- of four different foods. In addition, one of the mice was fed a certain drug. A short
- time later the mouse that was fed the drug became nervous and agitated. The
- researchers concluded that the drug caused the nervousness.[xi]
The only differentiating factor between the mice was the drug. The idea is to eliminate certain conditions as possible causes, just as in the other methods.
One sees that in occurrence 1 A, B, C, D and E are present while the phenomenon is present. In occurrence 2 only A, B, C, D are present and the phenomenon is absent. A sufficient condition is identified. The method of difference differs from the inverse method of agreement because the conclusion is less general. In other words, here “the conclusion applies directly only to the specific occurrence in which the phenomenon is present, whereas in the inverse method of agreement it applies to all the occurrences listed.”[xii] Notice that the method of difference makes use of particular instances and establishes a kind of probability, though one based on the specific instance used in the argument. One must keep in mind the likelihood that two occurrences will be precisely the same. The need to verify the repeat-ability of the conditions that the hypothesis concerns is the reason experiments like this are repeatedly performed and verified by different laboratories. The differences can be slight or great and the results possibly will be quite different. A thesis that may be experimented upon and rejected is falsifiable, meaning any given thesis can be verified or rejected by these given inductive methods. A new hypothesis replaces the old: progress. The effect of any given difference is unknown, so much can rely on only a few – seemingly insignificant – changes. Also, one cannot take into account each and every element that may go into an experiment like this one. One would need all possible elements of a given cause and effect in order to make an absolute determination, and that is obviously impossible. The degree to which one can exhaust all the possibilities is related to the degree to which one can be certain. One can use this method with the absence of a given element in order to obtain fruitful results. An example:
- Two identical white mice in a controlled experiment were fed identical diets. In
- addition, both were given vitamins A, B and C. One of the mice was also given
- vitamin D while the other was not. The mouse that was not fed vitamin D
- developed rickets, but the other one did not. The researchers concluded that
- the lack of vitamin D caused the rickets.[xiii]
The only real difference here is that one counts the absence of vitamin D as a kind of presence. In other words, the fact that there is no vitamin D is what caused the rickets and so one can say that vitamin D prevented the rickets. The same kind of probabilities and critiques can be said about the method of difference used with the absence of something as when the method is used with the presence of something.
The Joint Method of Agreement and Difference combines the direct method of agreement with the method of difference. This method identifies elements that are both necessary and sufficient, since the direct method identifies the necessary element while the method of difference identifies the sufficient element. An example:
- George, who exercised regularly, took vitamins, and got plenty of rest,
- contracted a rare disease. Doctors administered an antibiotic and the disease
- cleared up. Convinced that the cure was caused by either the exercise, the
- vitamins, the rest, or the antibiotic, the doctors searched for analogous cases.
- Among the two that were found, one got no exercise, took no vitamins, and got
- little rest. He was given the same antibiotic and was cured. The other person,
- who did the same things George did, was given no antibiotic and was not cured.
- The doctors concluded that George was cured by the antibiotic.[xiv]
The joint method of agreement is more general because it pertains to all the occurrences in the experiment. Occurrence 2 eliminates A, B and C as elements because they are absent when the phenomenon is present. This is the direct method of agreement. Occurrence 3 eliminates A, B and C as sufficient causes because they are present when the phenomenon is absent. The conclusion concerns the particular case of George and so pertains only to George's specific circumstances. One may claim then only that this experiment cured George, but as long as there exist characteristics similar to George but found in other men, the results will be the same. The more similar the characteristics that others have to George, the more likely will the antibiotic cure them as well. So, there is only a probability that the antibiotic will work.
Finally, the Method of Concomitant Variation matches elements' variations in one element with variations with another. This method is used when it is not possible that an element be completely present or absent. Increases of one element are matched with increases in another element and decreases in one element are matched with decreases in another element. Also increases can be matched to decreases and decreases matched to increases.
- ABC is coincident with abc
- AB + C is coincident with ab + c
- AB – C is coincident with ab – c
Therefore, B is causally connected to b. This graphic signifies any of the above: increases matched to increases, decreases matched to decreases, increases matched to decreases or decreases matched to increases. This method establishes the probability that some one element has a causal relation to another element. It is not clear what that relationship is precisely because the complete causes and effects are not present as with the other methods, but one can establish some causal connection, no matter what the probability is. Because there are not more rigorous comparisons and because the connection between elements is unknown, the argument here is probable. And, it is difficult to determine the level of probability as well.
Summation
We have seen what amounts to several significant pillars of scientific inquiry: inductive and deductive reasoning (both modern and ancient versions), definitions of types of causes and methods of verification of the causes, the necessity of falsifiable hypotheses. Science uses more than these things, depending on what a particular science investigates, but we have a good, working idea of what constitutes reasoning and verification. There are observations of nature that lead researchers to speculate on what is the “law” of nature that operates in a given occurrence of something. These are empirical aspects – in the form of recognized patterns – that assist in knowing what will happen; they are perceptions that come from experience and our senses. We use these pieces of information in order to make arguments and apply them to the world in the form of controlled experimentation. We form hypotheses with our reasoning and test the hypothesis, using one or more of the above methods for verifying cause and effect perhaps. Researchers suppose that there is a certain probability X will happen when Y happens. They then form notions about how nature will act and these notions are inductive in the modern sense; there are certain probabilities that Y will occur when X happens. Thus, researchers suspect that they know what will happen when certain conditions are met, or perhaps they reason in the form of a language-based argument or a mathematical calculation. Naturally, they need the strongest arguments possible in order to make the best possible inference about material reality. They thus need some foundation for their arguments that no-one disputes, or at least that everyone is able to accept.
As ancient thought progressed, mathematicians and philosophers found what we now call constants. These are accepted aspects of material reality or mathematical calculations give thinkers starting points from which they can draw inferences about the patterns seen in nature and how they may be predicted. These constants are things like the Pythagorean theorem, the calculation of π, sine, cosine and tangent, as well as the calculation of the area of a circle. Constants allow thinkers to have an anchor such that systematic reasoning becomes more potent. The development of argumentation in science relies upon these accepted truths. We will see how ancient thinkers first speculated about the nature of material reality and then questioned the answers that other thinkers gave. Generally, ancient thinkers engaged in reasoned arguments and not in empirical verification. There are, of course, empirical elements to every kind of reasoning, but ancient thinkers in general thought that reasoning itself was more potent and more true than mere observation. There was a slow but regular progress in the development of what we call science, but it was not concerted in its efforts the way science is today. Progress of ancient “science” was intermittent. We will review a number of thinkers in order to discern what pieces of science they employed, but we are only reviewing interpretations of some possible arguments of each, since believing the definitive argument to be found is to cease thinking. We do not have enough evidence to argue definitively, but we want to discuss method and findings. Thus, we imagine a bit and look at some of the evidence, keeping in mind that ancient thought was not scientific and that ancient thought has its own merits. It is not inferior to science but rather ancient thought occupies another dimension of inquiry. We will use Aristotelian syllogisms to examine how ancient thinkers thought.
Beginning in the sixth century B.C. the ancient Greeks attempted to answer the questions scientists still seek to answer. They looked for fundamental first principles of things, and it was something material they initially thought was the first “element” of all things. These Greeks thought that the universe is inherently ordered and discernible with the mind. They thought the parts of the universe fit together almost like a machine and ancient Greeks thus thought that they were able to dissect and explain the workings of the universe. Yet, sixth-century Greeks were not the first to seek explanations for physical phenomenon. The poets explained the universe in terms of Gods who controlled natural forces, and other earlier civilizations attempted explanations of their own. These Gods the poets thought were appeaseable through sacrifice and thus humans could not only comprehend the universe but they could control it and predict what would occur, if the Gods could be asked to act in certain ways once given the proper sacrifice. So, we begin with two poets and explain the universe in their terms, but we ought to know what we seek in any given thinker because each one presents us with a different account of what is fundamental about the order of the universe. What we look for in a thinker are many things: inductive or deductive reasoning, first principles, constants, an hypothesis, mathematical reasoning, language-based logical reasoning, pattern-finding. So, ancient Greeks sought patterns; patterns are repeated instances of things; repeated instances of things are categories; categories are compared; comparisons of the categories show how the patterns overlap and the overlapping of the categories is the reasoning of the thinker. This kind of reasoning is scientific in that it finds patterns and determines how the patterns relate to one another. Here is a significant portion of science and each thinker will possess some piece of science, like an explanation as to what element is the most fundamental. Thales, by example, seems to have thought that material reality was composed of water in various forms. We will review and then analyze some aspect of thought for each thinker. We do not have space or time to investigate every aspect of every thinker, but we will attempt to draw some essential insight from each. Because these ancient Greeks were physicists, we will look to understand how their notion of material reality operated. We look for how their arguments worked and what, if any, empirical aspect of their thought existed. We will then get some idea of what ancient “science” was, though there really was no such thing in the complete sense.
- [i] Pullman, Bernard. 1998. The Atom in the History of Human Thought. New York, Oxford, 6.
- [ii] Lloyd, G.E.R. Demystifying Mentalities. Cambridge, 1990, 29.
- [iii] French, R.K. Ancient Natural History. London, 1994, xiii.
- [iv] Aristotle claims as much in various places: “there is a knowledge of being qua being…” (Metaphysics IV, 1), “substance is the subject of our inquiry” (Metaphysics XII, 1), “Nature is a principle of motion and change and it is the subject of our inquiry” (Physics III, 1), et alia.
- [v] For a review of induction and deduction in modern science, see Sambursky, S. 1956. The Physical World of the Greeks. New York.
- [vi] The section that concerns causality comes from Hurley, Patrick J.A Concise Introduction to Logic.
- [vii] The following conditional statements are taken from Hurley's A Concise Introduction to Logic, 487. The examples that follow are modified versions of those given in A Concise Introduction to Logic.
- [viii] These are John Stuart Mill's methods. We use these explanations of cause and effect because they fit more easily into the ancient framework of thinking. Modern methods are more complicated and in some ways better, but Mill's methods make clear the connection the ancient world has to the modern one. What we review are not precisely the same methods Mill produced, but they will give us a better connection to the ancient way of reasoning. We may thus better compare and understand how ancient thinking is “scientific.” There is no claim that the whole of scientific reasoning is here represented, but these methods provide some contextualization of modern science and contrast with ancient inquiry.
- [ix] The following tables are all taken from Hurley’s Concise Introduction to Logic.
- [x] This example is a modified version of one that comes from Hurley’s Concise Introduction to Logic, p 493.
- [xi] This example was taken from Hurley’s Concise Introduction to Logic, p 493.
- [xii] Hurley, p. 495.
- [xiii] Hurley, p. 495.
- [xiv] Hurley, p. 496.